はじめに
メーカーの製造ラインにおいては、古典的な方法であるシューハートの管理図で工程を管理しているところはまだまだ多いですが、異常の検出に時間がかかる問題も指摘されています。近年、AIによる異常検知技術が進んでおり、製造ラインにおいても各種センサーを設備に取り付けて、タイムリーに工程の異常を検知する取り組みが盛んです。
様々な異常検知の手法が研究されていますが、今回は時系列解析による異常検知のやり方を見ていきます。
時系列データの異常検知
1) 時系列データの異常について
時系列データを扱う場合、隣り合う時刻の観測値同士には相関があり、その相関関係を無視するわけにはいきません。
時系列データの異常パターンの例を図1に示します。なお、データは以下を用いています。パターン1)Rに標準で搭載されているriverデータです。ここからダウンロードできます(ファイル名:rivers.csv)。パターン2)3)人工的に作成した正弦波。
import pandas as pd
import numpy as numpy
import matplotlib.pyplot as plt
np.random.seed(seed=10)
data_1 = pd.read_csv("rivers.csv")
fig = plt.figure(figsize=(16, 4))
ax1 = fig.add_subplot(1, 3, 1)
ax1.plot(data_1.iloc[:,1], marker="o", linestyle="None")
ax1.set_title("Pattern 1")
data_2x = np.linspace(0, 2*np.pi, 150)
data_21y = np.sin(2*data_3x)+0.05*np.random.randn(len(data_3x))
data_22y = np.sin(6*data_3x)+0.05*np.random.randn(len(data_3x))
data_23y = np.sin(2*data_3x)+0.05*np.random.randn(len(data_3x))
data_2y = np.concatenate([data_21y, data_22y, data_23y])
ax2 = fig.add_subplot(1, 3, 2)
ax2.plot(data_2x, data_2y)
ax2.set_title("Pattern 2")
data_3x = np.linspace(0, 2*np.pi, 50)
data_3y = np.sin(data_3x)+0.05*np.random.randn(len(data_3x))
data_3y[35:37] = data_3y[35:37] + 0.7
ax3 = fig.add_subplot(1, 3, 3)
ax3.plot(data_3x, data_3y, marker="o", linestyle="None")
ax3.set_title("Pattern 3")
plt.show()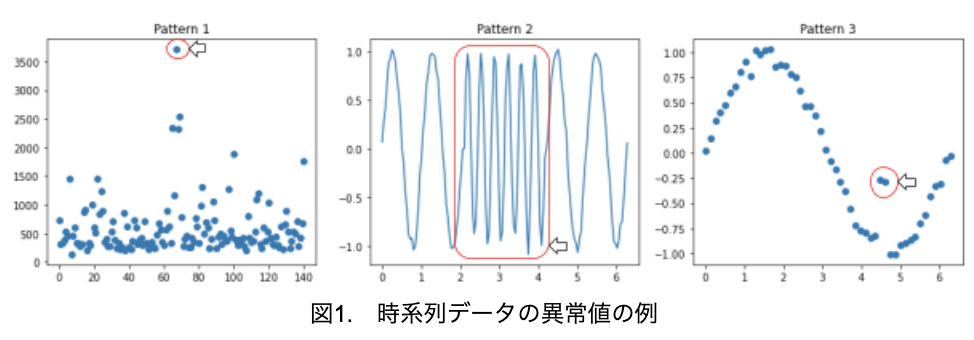
パターン1、3は外れ値、パターン2は周期の変化の異常が見られます。パターン1の異常であれば、データの順番を変えても異常を検出できますが、パターン2と3はデータの順番を変えると、異常と判断できなくなります。このことは、前の時刻の観測値との関係が異常の判定に重要であることを意味しています。よって、各観測値をそれぞれお互いに独立(無関係)と考えると、異常の検出が困難となるため、時系列データとしての異常判定が必要になります。
2) 時系列データの異常検知に用いるデータ
それでは、実際のデータを使って、時系列データの異常検知を行ってみます。使うデータは、Rに標準で搭載されているnottemデータです。ここからダウンロードできます(ファイル名:nottem.csv)。このデータは、イギリスのノッティンガム城で記録された、1920年から1939年にわたる20年分の月次平均気温(華氏)のデータです。
まずは、全体のデータを見てみましょう(図2)。
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv("nottem.csv", index_col=0)
fig = plt.figure(figsize=(15, 4))
ax1 = fig.add_subplot()
ax1.plot(data.iloc[:,1])
ax1.set_title("Temperature")
plt.show()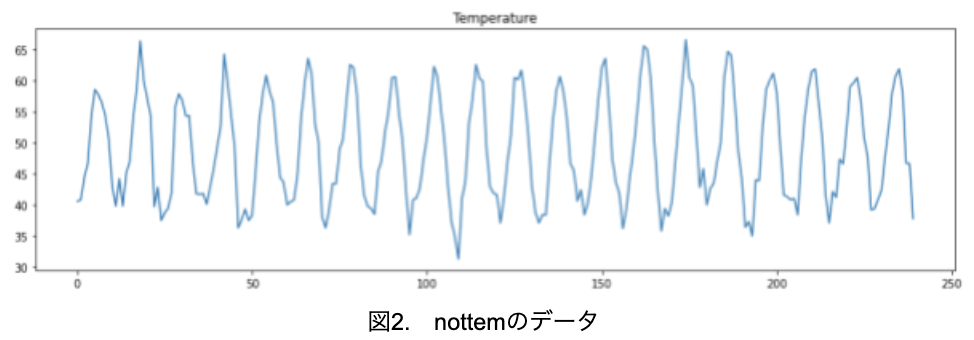
気温のデータということもあり、周期的に変化していることが分かります。図2を見ると、ある値を中心に上下に均等に振れているので、定常過程と見ることができそうです。念のため、ADF検定で定常性を確認しておきます。
import statsmodels.api as sm
# 単位根検定(ADF検定)
adf_result = sm.tsa.stattools.adfuller(data["value"])
adf_resultp値は1.8%なので、有意水準5%で帰無仮説を棄却し対立仮説を採択します。ADF検定では帰無仮説が単位根過程、対立仮説は定常過程なので、今回のデータは定常過程とみなせることが統計的に確認できました。
定常過程に有効なモデルは、MAモデル、ARモデル、ARMAモデルがありますが、一番汎用性の高いARMAモデルで予測モデルを作り、異常検知をしてみます。図2を見るとパターンに乱れが見られるので、その部分を異常として検出することを狙います。具体的には、訓練用データを使ってARMAモデルで予測モデルを作り、確率を基にデータが存在し得る範囲を決め、そこから外れたデータを異常と検出する方法を検討していきます。
3) 時系列データの異常検知
それでは、図2のデータのうち前半の120個を訓練用データとし、後半の120個をテスト用データとします。
訓練用データでモデル式を作ります。
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv("nottem.csv", index_col=0)
train = data.iloc[:120,1]
test = data.iloc[120:,1]
#次数の推定
import statsmodels.api as sm
jisu = sm.tsa.arma_order_select_ic(train, max_ar=2, max_ma=2, ic='aic')
# ARMAモデルの作成と推定
model = sm.tsa.ARMA(train, order=(jisu.aic_min_order[0], jisu.aic_min_order[1]))
result = model.fit(trend="c", method="css-mle")
print(result.summary())ARMA Model Results
========================================================================
Dep. Variable: value No. Observations: 120
Model: ARMA(2, 2) Log Likelihood -303.491
Method: css-mle S.D. of innovations 2.684
Date: Mon, 13 Apr 2020 AIC 618.982
Time: 09:03:41 BIC 635.707
Sample: 0 HQIC 625.774
========================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------
const 48.7237 0.021 2294.863 0.000 48.682 48.765
ar.L1.value 1.7322 0.001 2294.676 0.000 1.731 1.734
ar.L2.value -1.0000 nan nan nan nan nan
ma.L1.value -1.6359 nan nan nan nan nan
ma.L2.value 0.9058 nan nan nan nan nan
Roots
========================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------
AR.1 0.8661 -0.4998j 1.0000 -0.0833
AR.2 0.8661 +0.4998j 1.0000 0.0833
MA.1 0.9030 -0.5372j 1.0507 -0.0854
MA.2 0.9030 +0.5372j 1.0507 0.0854
------------------------------------------------------------------------最適の次数(p, q)=(2,2)でARMAモデルを作成しています。では、作成したモデルで、訓練用データの実測値と予測値をプロットしてみましょう(図3)。
fig = plt.figure(figsize=(10, 4))
ax1 = fig.add_subplot()
ax1.plot(train, label="Observed")
ax1.plot(result.predict(start=0, end=119), label="Predicted")
ax1.legend()
plt.show()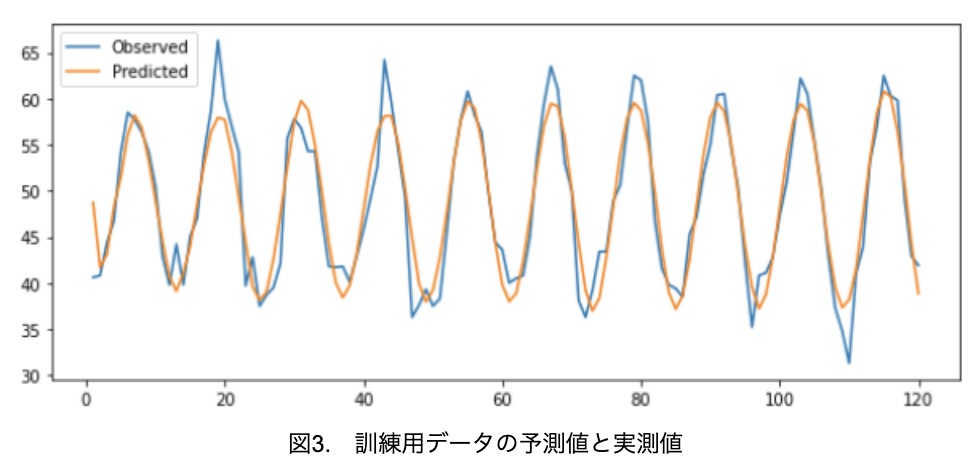
まずまず予測できているように見えますね。それでは、作成したモデルで未知のテスト用データを予測してみます。
#テスト用データの予測値
predict_testdata = result.forecast(steps=120)[0]
#テスト用データの95%信頼区間
predict_testci = result.forecast(steps=120)[2]
fig2 = plt.figure(figsize=(10, 5))
ax2 = fig2.add_subplot()
ax2.plot(test.to_numpy(), label="Observed", marker="o")
ax2.plot(predict_testdata, label="Predicted")
ax2.fill_between(x=np.arange(0, 120),y1=predict_testci[:,0], y2=predict_testci[:,1], color="green", alpha=.1, label="95% confidence interval")
ax2.set_ylim([20,80])
ax2.legend(loc="upper left", borderaxespad=0)
plt.show()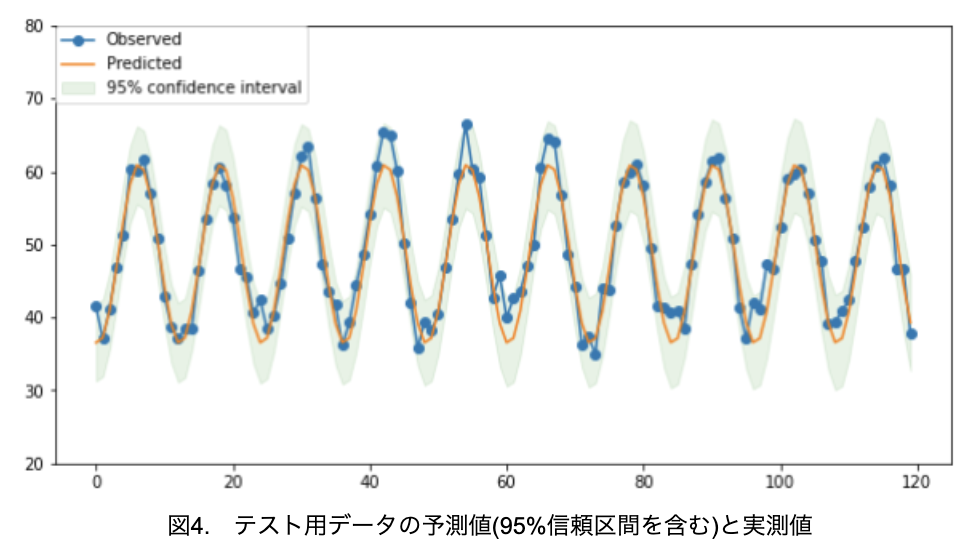
ここで、95%信頼区間を正常範囲とし、これを越えたら異常と判断すると定義をします。すると、異常検知することができます(図5)。
#95%信頼区間を越えるデータを異常とみなし、色を変える
fig3 = plt.figure(figsize=(10, 5))
ax3 = fig3.add_subplot()
for i in range(len(test)):
ax3.plot(np.arange(0, 120)[i], test.to_numpy()[i], marker="o",
color="blue" if predict_testci[i,0]<=test.to_numpy()[i]<=predict_testci[i,1] else "red")
ax3.plot(test.to_numpy(), color="blue", label="Observed")
ax3.fill_between(x=np.arange(0, 120),y1=predict_testci[:,0], y2=predict_testci[:,1], color="green", alpha=.1, label="95% confidence interval")
ax3.set_ylim([20,80])
ax3.legend(loc="upper left", borderaxespad=0)
plt.show()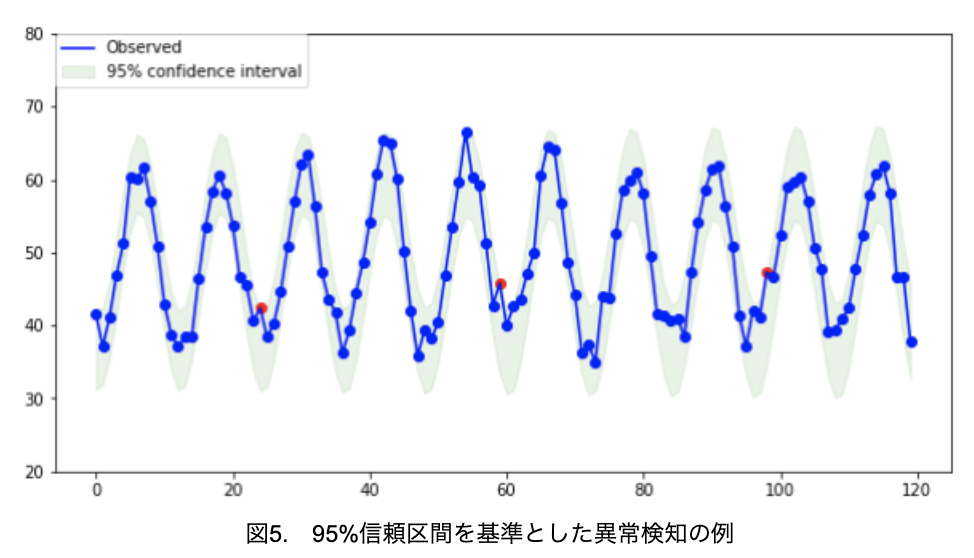
信頼区間を越えるデータを3点検出できました。パターンの乱れが何か所か見られましたが、おおよそのデータは95%の信頼区間内に入っているようです。
今回は95%信頼区間を正常の範囲としましたが、異常を素早く検知したいのであれば90%信頼区間を使ったり、よほどのことがない限り異常を検知したくないのであれば99%信頼区間を使ったりすることで、異常検出力の調整が可能です。
おわりに
今回は、時系列解析よる異常検知の例を紹介しました。今回のデータではARMAモデルがうまくフィットしましたが、データによっては、ARIMAモデルやSARIMAモデルを使う必要があるでしょう。様々なモデルからデータに合った最適のモデルを選定し、異常検知に使ってみてください。
参考サイト
ローカルレベルモデルを用いた時系列データに対する異常検知
https://qiita.com/hrkz_szk/items/ea082ca07460ab8b8813
piponではエンジニアの皆様に業務委託や副業でAI・データサイエンスの案件をご紹介しています!
piponの案件にご興味がある方は以下のフォームにご登録ください。案件をご案内します。 https://share.hsforms.com/1qk0uPA_lSu-nUFIvih16CQegfgt


