はじめに
今回は、様々な時系列データの解析手法のうち、ARIMAモデルとSARIMAモデルを紹介します。
ARIMAモデルとは、autoregressive integrated moving averageの略で、自己回帰モデル(ARモデル)、移動平均モデル(MAモデル)、和分モデル(Iモデル)の3モデルを組み合わせたモデルです。ARIMAモデルは、自己回帰和分移動平均モデルとも呼ばれます。
SARIMAモデルとは、Seasonal AutoRegressive Integrated Moving Averageの略で、ARIMAモデルに「季節的な周期パターン」を加えたモデルです。
ARIMAモデルとSARIMAモデルは、非定常過程のデータに対して適用できるのが大きな特徴です。
ARIMAモデルやSARIMAモデルを理解するには、MAモデル、ARモデル、ARMAモデルの理解が必要となりますので、事前にそれらを簡単に見ておきます。
MAモデル
MAモデルとは移動平均(Moving Average)モデルのことです。1次MAモデルを例に取ってMAモデルを考えてみましょう。
1次MAモデルは
yt = c + εt + θ1εt−1
の式で表されるモデルです。ここでεtは時点tにおけるホワイトノイズです。ホワイトノイズとは、時点tによって発生するランダムな数と思ってください。
1 次MAモデルでは、1時点前までのホワイトノイズを用い、n次MAモデルであれば、n時点前までのホワイトノイズを用います。
1次MAモデルでは、yt-1=c + εt-1 + θ1εt−2が成り立ち、ytとyt-1でεt-1という共通項を持つことが分かります。これは、ytとyt-1の間に相関が生じることを意味しており、1次自己相関を持つと言います。
では、1次MAモデルの例をいくつか見てみましょう(図1)。
import numpy as np
import matplotlib.pyplot as plt
theta = [-0.9, -0.5, 0.5, 0.9]
sigma = [0.5, 2]
c = 0
sample = 100
fig = plt.figure(figsize=(15, 5))
fig.subplots_adjust(hspace=0.5, wspace=0.2)
for k in range(len(sigma)):
for j in range(len(theta)):
noize = np.random.normal(loc=0, scale=sigma[k], size=sample+1)
y0 = 0
y = np.zeros(sample+1)
y[0] = y0
for i in range(sample):
y[i+1] = c+noize[i+1]+theta[j] * noize[i]
y= y[1:]
ax = fig.add_subplot(2, 4, 1+j+4*k)
ax.set_title("c = 0, θ = {}, ε = {}".format(theta[j], sigma[k]))
ax.plot([int(i) for i in range(1, sample+1)],y)
plt.show()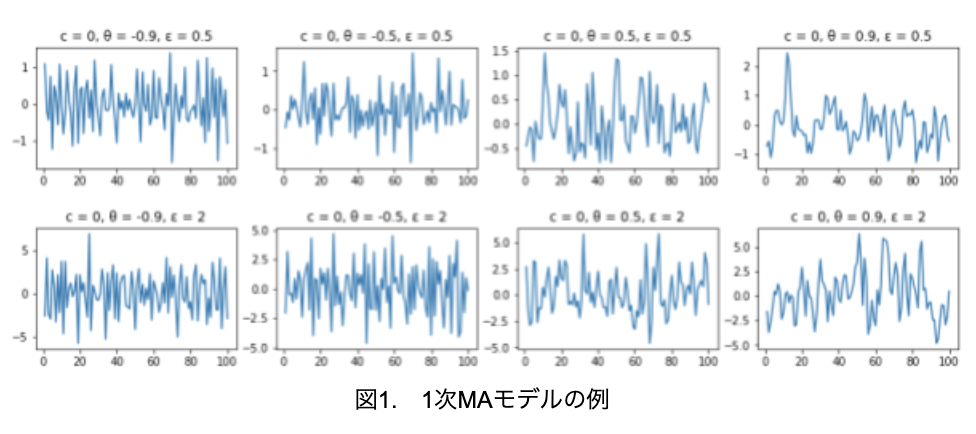
上段がε=0.5、下段がε=2なので、下段の方が振幅が大きくなっています。そして、左から右に向かってθ1が大きくなっています。符号が負であるとギザギザしており、符号が正であると滑らかになっています。これは符号が正の場合、1次の正の自己相関が生じるので、ytとyt-1は同じ方向に動く傾向となります。そして符号が負の場合、1次の負の自己相関が生じるので、ytとyt-1は逆方向に動く傾向となるためです。
また、ここでは詳しく述べませんが、MAモデルは期待値と自己共分散が時点tに依存していないので、MAモデルはいかなるパラメータを設定しても、定常過程であるという特徴があります。
3. ARモデル
ARモデルとは自己回帰(AutoRegressive)モデルのことです。1次ARモデルを例に取ってARモデルを考えてみましょう。
1次ARモデルは
yt = c + Φ1yt−1 + εt
の式で表されるモデルで、1時点前のデータとホワイトノイズから成り立っています。ytの式にyt-1の項が含まれているので、ytとyt-1が相関を持つことが明らかに分かります。
では、1次ARモデルの例をいくつか見てみましょう(図2)。
import numpy as np
import matplotlib.pyplot as plt
phi = [-1.1, -0.8, -0.2, 0.2, 0.8, 1.1]
sigma = [0.5, 2]
center = 0
sample = 100
fig = plt.figure(figsize=(16, 6))
fig.subplots_adjust(hspace=0.5, wspace=0.4)
for k in range(len(sigma)):
for j in range(len(phi)):
noize = np.random.normal(loc=0, scale=sigma[k], size=sample+1)
y0 = 0
y = np.zeros(sample+1)
y[0] = y0
for i in range(sample):
y[i+1] = center + phi[j] * y[i] + noize[i]
y= y[1:]
ax = fig.add_subplot(2, 6, 1+j+6*k)
ax.set_title("c = 0, Φ= {}, ε = {}".format(phi[j], sigma[k]))
ax.plot([int(i) for i in range(1, sample+1)],y)
plt.show()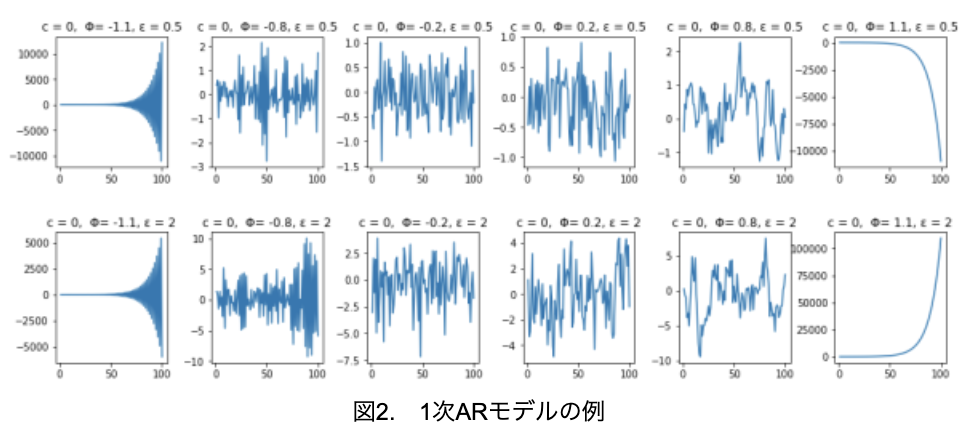
上段がε=0.5、下段がε=2なので、1次MAモデルと同じく下段の方が振幅が大きくなっています。そして、両端のグラフと2~5列目のグラフで明らかに違うことが分かります。2~5列目のグラフは、1次MAモデルのように、上下方向に万遍なくばらついており、定常性を有していることがうかがえます。それに対して、両端のグラフは明らかな傾向が見て取れ、定常性を有していない、つまり、非定常なモデルとなっています。
1次ARモデルの場合、|Φ1|<1のとき定常過程となり、|Φ1|≧1のとき非定常となるという特徴がありますが、グラフを見れば一目瞭然です。
ARMAモデル
次は、ARMAモデルを見ていきます。これは自己回帰移動平均(AutoRegressive Moving Average)モデルのことで、名前の通り、これまで見てきたARモデルとMAモデルを組み合わせたモデルです。
(p, q)次ARMAモデルを一般式で表すと、
yt = c + Φ1yt−1 + … + Φpyt−p + εt + θ1εt−1 + … +θqεt−q
で定義できます。
ARモデルにMAモデルを加えたことでモデル式の柔軟性が高まり、定常過程の時系列データに対しては、非常に強力な説明力・予測力を持っているのが大きな特徴です。
MAモデルは常に定常性を有していますので、ARMAモデルが定常過程かどうかはARモデルが定常過程かどうかに依存します。
では、(1,1)次ARモデルの例をいくつか見てみましょう(図3)。なお、Φ以外のパラメータは、θ1=0.4、ε=2に固定しています。
import numpy as np
import matplotlib.pyplot as plt
phi = [-1.1, -0.8, -0.2, 0.2, 0.8, 1.1]
theta = 0.4
sigma = 2
center = 50
sample = 100
fig = plt.figure(figsize=(16, 3))
fig.subplots_adjust(hspace=0.5, wspace=0.4)
for j in range(len(phi)):
noize = np.random.normal(loc=0, scale=sigma, size=sample+1)
y0 = center
y = np.zeros(sample+1)
y[0] = y0
for k in range(sample):
y[k+1] = center + phi[j] * y[k] + noize[k+1] + theta*noize[k]
y= y[1:]
ax = fig.add_subplot(1, 6, 1+j)
ax.set_title("Φ= {}".format(phi[j]))
ax.plot([int(i) for i in range(1, sample+1)],y)
plt.show()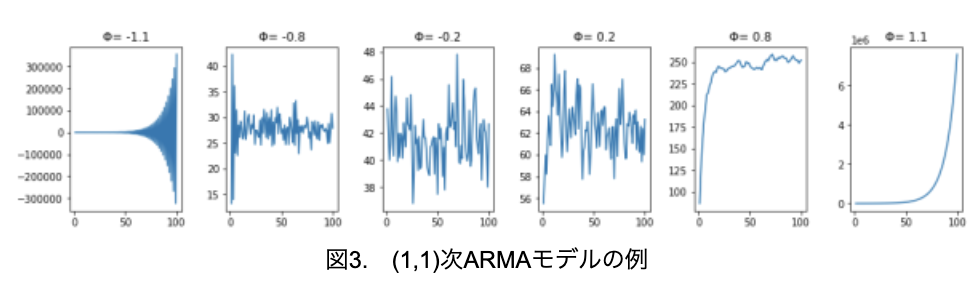
MAモデルは常に定常のため、ARモデルと同じく、|Φ1|<1のとき定常過程となり|Φ1|≧1のとき非定常となっていることが分かります。ARMAモデルはMAモデルとARモデルを組み合わせているため、定常過程のデータに対しては、かなり精度よく予測が可能です。そこで、図3の左から2番目のデータを使って、各パラメータを予測してみましょう。
#データの作成
import numpy as np
import matplotlib.pyplot as plt
phi = -0.8
theta = 0.4
sigma = 2
center = 50
sample = 100
noize = np.random.normal(loc=0, scale=sigma, size=sample+1)
y0 = center
y = np.zeros(sample+1)
y[0] = y0
for k in range(sample):
y[k+1] = center + phi * y[k] + noize[k+1] + theta*noize[k]
y= y[1:]
#パラメータの予測
#次数の推定
import statsmodels.api as sm
print(sm.tsa.arma_order_select_ic(y, max_ar=2, max_ma=2, ic='aic')){'aic': 0 1 2
0 579.283912 524.044364 508.941711
1 472.735539 467.073436 468.476308
2 469.536316 468.710843 469.834314, 'aic_min_order': (1, 1)}まずは、ARMAモデルの次数をAICで推定します。今回の解析は、うまく(1,1)次と推定できました。
そこで、(1,1)次ARMAモデルを作成し、パラメータを推定します。
# ARMAモデルの作成と推定
model = sm.tsa.ARMA(y, order=(1, 1))
result = model.fit()
print(result.summary())ARMA Model Results
========================================================================
Dep. Variable: y No. Observations: 100
Model: ARMA(1, 1) Log Likelihood -229.537
Method: css-mle S.D. of innovations 2.369
Date: Fri, 03 Apr 2020 AIC 467.073
Time: 00:11:21 BIC 477.494
Sample: 0 HQIC 471.291
========================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------
const 27.6869 0.162 170.739 0.000 27.369 28.005
ar.L1.y -0.9846 0.021 -45.991 0.000 -1.027 -0.943
ma.L1.y 0.3547 0.109 3.250 0.002 0.141 0.569
Roots
========================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------
AR.1 -1.0157 +0.0000j 1.0157 0.5000
MA.1 -2.8190 +0.0000j 2.8190 0.5000
------------------------------------------------------------------------
データの実際のパラメータΦ1= -0.8, θ1=0.4, ε=2に対し、推定値はΦ1= -0.98, θ1=0.35, ε=2.369となり、当たらずといえども遠からずな結果が得られました。サンプル数が100だったので、もう少しデータを多くすれば、推定精度は上がるかもしてません。
以下のコードで、実測値と推定値のグラフを描けます。
result.plot_predict()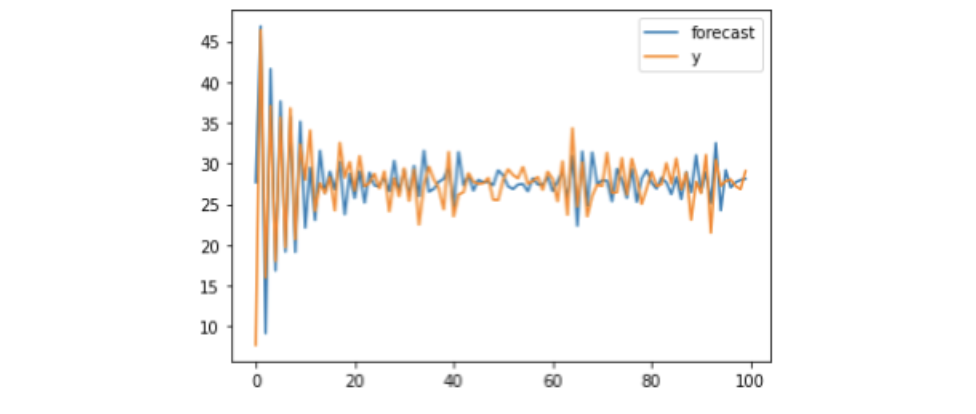
なお、図3の一番左または右の非定常のデータで、同じようにARMAモデルでパラメータの推定を行おうとすると、エラーとなります。ARMAモデルは、定常過程の時系列データしか解析できないことを覚えておいてください。
ARIMAモデルとは
定常性を有する時系列データに対しては、ARMAモデルがパラメータの推定に有効であることが分かりました。
しかし、定常過程でない、非定常なデータに対してはARMAモデルは無力です。そこで、非定常な時系列データに有効なモデルの一つである、ARIMAモデルを見ていきます。
世の中には、日経平均株価の推移など定常過程の性質を持たない、非定常なデータを得られることの方が多いので、それらのデータ解析に向いているモデルです。
これまで見てきた定常過程は、トレンドがないことと平均回帰性が主な性質ですが、定常過程の持つ性質を満たさないデータをモデル化する際に有効な考え方が、「単位根過程」です。単位根過程は非定常過程の代表であり、原系列(元データ)ytが非定常過程で、差分系列Δyt=yt-yt-1が定常過程であるとき、その過程を単位根過程と呼びます。
単位根過程は1次和分過程(1次Iモデル)とも呼ばれ、その差分系列が(p,q)次ARMAモデルで表されるとき、単位根過程は(p,1,q)次ARIMAモデル(自己回帰和分移動平均)と呼ばれます。一般に、d階差分を取った系列が(p,q)次ARMA過程に従う過程を(p,d,q)次ARIMAモデルと呼びます。
一言で述べると、データの差分を取ってからARMAを適用したモデルが、ARIMAモデルということになります。
それでは、単位根過程データを人工的に作り、そのデータをARIMAモデルで解析してみましょう。
まず、解析用のデータを、下記の式に従い(1, 1, 1)次ARIMAモデルで作成します。Φ1=1なので、このデータは非定常であることが分かります。
yt = 1+ yt−1 + εt - εt−1
そしてこの式を変形すると、
Δyt=yt-yt-1 = 1 + εt - εt−1
となるので、差分データΔytはc=1, θ1=-1の1次MAモデルであることが分かります。
#データの作成
import numpy as np
import matplotlib.pyplot as plt
phi = 1
theta = -1
sigma = 10
center = 1
sample = 200
noize = np.random.normal(loc=0, scale=sigma, size=sample+1)
y0 = center
y = np.zeros(sample+1)
delta_y = np.zeros(sample+1)
y[0] = y0
delta_y[0] = 0
for k in range(sample):
y[k+1] = center + phi * y[k] + noize[k+1] + theta*noize[k]
delta_y[k+1] = y[k+1] - y[k]
y = y[1:]
delta_y = delta_y[1:]
fig = plt.figure(figsize=(10, 3))
ax1 = fig.add_subplot(1, 2, 1)
ax1.set_title("c=1, Φ=1, θ=-1, ε=10")
ax1.plot([int(i) for i in range(1, sample+1)],y)
ax2 = fig.add_subplot(1, 2, 2)
ax2.set_title("delta_y data")
ax2.plot([int(i) for i in range(1, sample+1)],delta_y)
plt.show()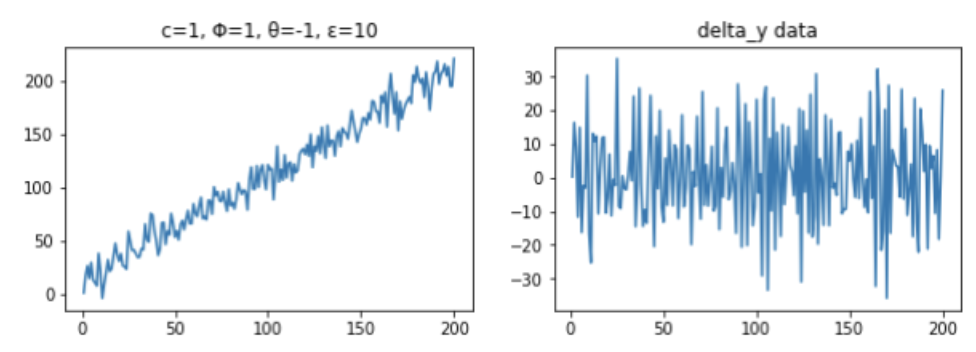
元データは右上がりのトレンドが見られますが、差分データは特にトレンドは見られず、0を中心に上下にばらついていることから、定常過程であることが分かります。
それでは、このデータを使ってARIMAモデルでパラメータを推定してみます。
import statsmodels.api as sm
for i in range(2): #0次と1次の和分過程で探索
delta_y = np.diff(y, n=i)
resdiff = sm.tsa.arma_order_select_ic(delta_y, ic="aic", trend="nc")
print(resdiff)0次和分過程
{'aic': 0 1 2
0 NaN 2237.244350 2073.501314
1 1615.698003 1530.025649 1530.031841
2 1552.847956 1529.986114 1533.685171
3 1553.196278 1552.800983 1532.931096
4 1544.370244 1533.666189 1535.477473, 'aic_min_order': (2, 1)}
1次和分過程
{'aic': 0 1 2
0 NaN 1515.417150 1515.424120
1 1538.361931 1515.378152 1517.307646
2 1525.871642 1517.371654 1519.240139
3 1518.737854 1519.060110 1520.164403
4 1520.168956 1519.165132 1521.732557, 'aic_min_order': (1, 1)}AICで最適パラメータを計算すると、1次和分過程の(p,q)=(1,1)のときにAICが最小となることが分かりました。従って、与えられた時系列データは、(1, 1, 1)次ARIMAモデルで精度よく推定できると思われます。
(1, 1, 1)次ARIMAモデルのパラメータを推定します。
from statsmodels.tsa.arima_model import ARIMA
arima_1_1_1 = ARIMA(y, order=(1, 1, 1)).fit(dist=False)
arima_1_1_1.summary()ARIMA Model Results
Dep. Variable: D.y No. Observations: 199
Model: ARIMA(1, 1, 1) Log Likelihood -737.442
Method: css-mle S.D. of innovations 9.788
Date: Fri, 03 Apr 2020 AIC 1482.885
Time: 08:13:42 BIC 1496.058
Sample: 1 HQIC 1488.216
coef std err z P>|z| [0.025 0.975]
const 0.9966 0.043 23.041 0.000 0.912 1.081
ar.L1.D.y 0.0103 0.085 0.121 0.904 -0.157 0.178
ma.L1.D.y -0.9477 0.051 -18.404 0.000 -1.049 -0.847
Roots
Real Imaginary Modulus Frequency
AR.1 96.9090 +0.0000j 96.9090 0.0000
MA.1 1.0551 +0.0000j 1.0551 0.0000ARIMAモデルのパラメータは、c=1.0, θ1=-0.95, Φ1=0.01, ε=9.79と推定できました。実測値は、c=1, θ1=-0.1, Φ1=1, ε=10なので、Φ1がうまく予測できませんでした。データ数を増やすなどすれば、精度は上がる可能性があります。
SARIMAモデルとは
最後に、SARIMAモデルを見ます。単位根過程に対しては、ARIMAモデルでまずまず予測することができますが、季節変動がある非定常データはARIMAモデルではうまくフィットしません。そこで、季節変動があるデータに対して有効なのが、ARIMAモデルを拡張したSARIMAモデルです。具体的には、時系列方向にARIMAモデルを使い、かつ、周期方向にもARIMAモデルを使っているモデルです。
最終的に、SARIMAモデルでは7つの次数を決めます。それは、時系列方向の(p, d, q)次ARIMAのp, d, q、周期方向の(P, D, Q)次ARIMAのP, D, Q、そして周期sの7つです。周期sはグラフを見て判断できることが多いです。
それでは、Rの時系列データ解析の例でよく用いられるAirPassengersのデータを使って、SARIMAモデルで実際に解析してみます。
それでは、AirPassengersのデータを読み込んで、生データを見てみましょう。
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv("AirPassengers.csv",
index_col="Month",
parse_dates=True,
dtype="float")
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.plot(data["#Passengers"])
ax1.set_title("Passengers trend")
ax1.set_xlabel("Year")
ax1.set_ylabel("Passengers")
plt.show()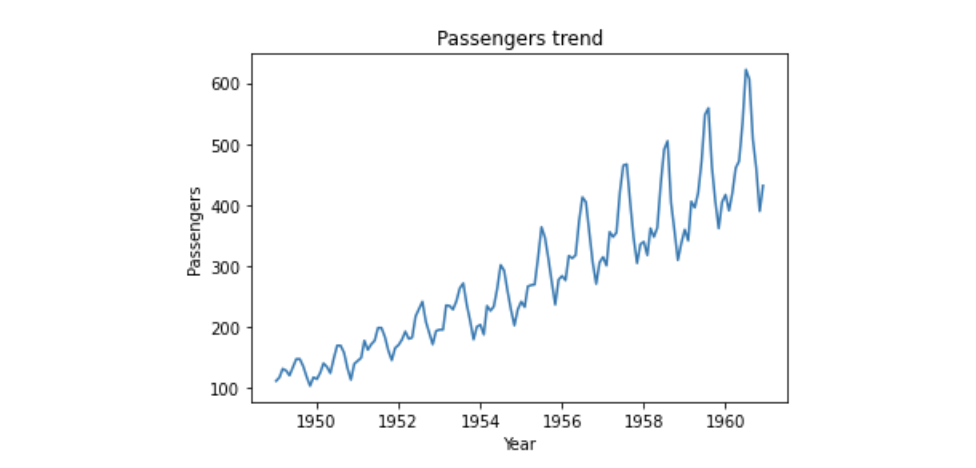
乗客数は右上がりになっており、増加傾向にあることが分かります。また、周期的に乗客数が変化していることも分かります。非定常過程となる要因は2つあり、1つはトレンド、もう1つは季節変動ですが、このデータは両者を含んでいることになります。
SARIMAモデルを使えば、モデル中の次数を設定することで、これまで述べてきたMAモデル、ARモデル、ARMAモデル、ARIMAモデルも表すことができますので、汎用性の高いモデルと言えます。それでは最後は機械学習らしく、SARIMAモデルで訓練用データで学習して未知のデータを予測してみたいと思います。
data_2 = np.log(data) #対数変化したデータを使う
train = np.log(data[:"1957-12-31"]["#Passengers"])
# 最適の次数を決めるため、グリッドサーチを行うための準備
import itertools
# 各パラメータの範囲を決める
p = d = q = range(0, 3) #時系列方向のARIMAモデルの次数(p, d, q)検討範囲
s_p = s_d = s_q = range(0, 2) #周期方向のARIMAモデルの次数(P, D, Q)検討範囲
# p, d, q の組み合わせを表すリストを作成
pdq = list(itertools.product(p, d, q))
# P, D, Q の組み合わせを表すリストを作成。周期は、グラフからs = 12としている。
pdq_season = [(x[0], x[1], x[2], 12) for x in list(itertools.product(s_p, s_d, s_q))]
from statsmodels.tsa.statespace.sarimax import SARIMAX
import warnings
warnings.filterwarnings("ignore") # warnings を表示させないようにする
# グリッドサーチで、最適の次数をAICで探索
min_aic = [0, 0, 10000]
for param in pdq:
for param_season in pdq_season:
try:
model_sarimax = SARIMAX(train,
order = param,
seasonal_order=param_season,
enforce_stationarity=True,
enforce_invertibility=True)
results = model_sarimax.fit()
print("order{}, s_order{} - AIC: {}".format(param, param_season, results.aic))
if results.aic < min_aic[2]:
min_aic = [param, param_season, results.aic]
except:
continue
print("\AICが最も良いモデル:", min_aic)
order(0, 0, 0), s_order(0, 0, 0, 12) - AIC: 672.2469661806601
order(0, 0, 0), s_order(0, 0, 1, 12) - AIC: 563.9682273977863
order(0, 0, 0), s_order(0, 1, 0, 12) - AIC: -95.22009529373264
・・・
order(2, 2, 2), s_order(1, 1, 0, 12) - AIC: -320.52715587583884
order(2, 2, 2), s_order(1, 1, 1, 12) - AIC: -324.3508043456799
\AICが最も良いモデル: [(1, 1, 1), (1, 0, 1, 12), -361.46473041738244]総当たりでの探索で、最適の次数は(p, d, q, P, D, Q, s)=(1, 1, 1, 1, 0, 1, 12)と決まりました。
SARIMAモデルの次数が決まったので、最適条件で予測モデルを作成します。
model_final = SARIMAX(train,
order = min_aic[0],
seasonal_order=min_aic[1],
enforce_stationarity=True,
enforce_invertibility=True)
results = model_final.fit()
print(results.summary())SARIMAX Results
======================================================================
Dep. Variable: #Passengers No. Observations: 108
Model: SARIMAX(1, 1, 1)x(1, 0, 1, 12) Log Likelihood 185.732
Date: Mon, 06 Apr 2020 AIC -361.465
Time: 16:15:46 BIC -348.101
Sample: 01-01-1949 HQIC -356.047
- 12-01-1957
Covariance Type: opg
======================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------
ar.L1 0.5238 0.187 2.805 0.005 0.158 0.890
ma.L1 -0.8079 0.137 -5.918 0.000 -1.075 -0.540
ar.S.L12 0.9909 0.008 120.690 0.000 0.975 1.007
ma.S.L12 -0.6276 0.123 -5.115 0.000 -0.868 -0.387
sigma2 0.0014 0.000 7.204 0.000 0.001 0.002
======================================================================
Ljung-Box (Q): 37.92 Jarque-Bera (JB): 6.69
Prob(Q): 0.56 Prob(JB): 0.04
Heteroskedasticity (H): 0.38 Skew: -0.03
Prob(H) (two-sided): 0.00 Kurtosis: 4.22
======================================================================
構築したモデルの妥当性を評価するために、残差を確認します。残差とは、予測値と実測値の差です。残差にクセがなくランダムであれば、作成したモデルはまずまずと言えます。
results.plot_diagnostics(figsize=(10,8), lags=20)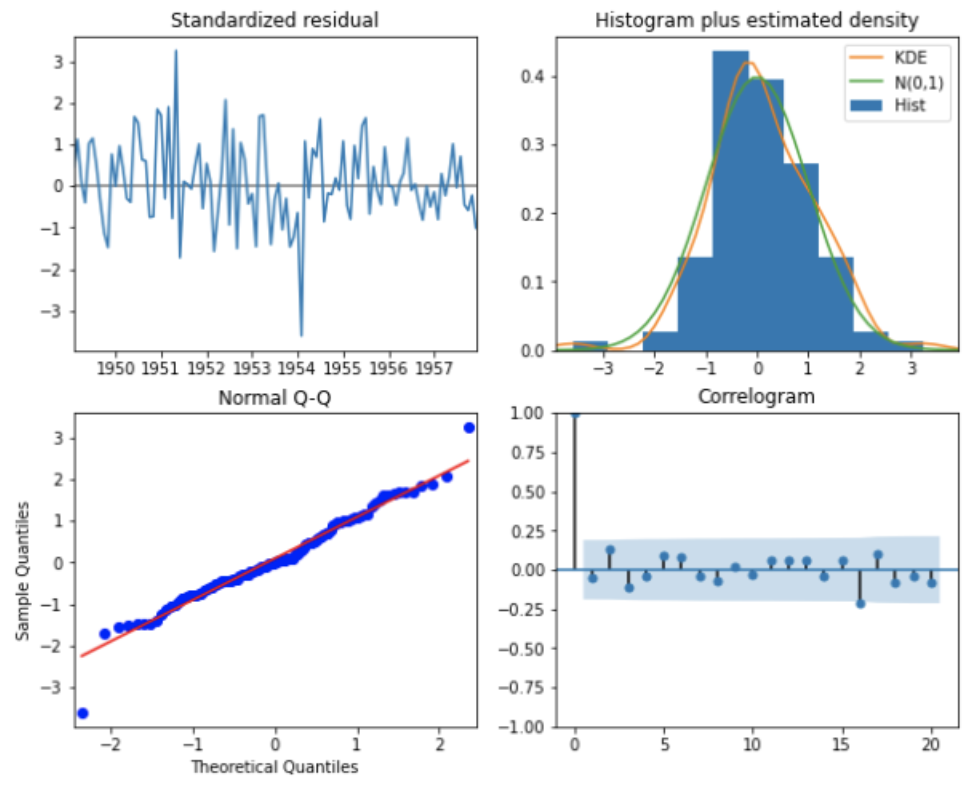
左上:標準化残差のプロット、右上:標準化残差のヒストグラム、左下:標準化残差のQ-Qプロット、右下:標準化残差の自己相関係数です。残差には特に特徴や傾向は見られないので、作成したモデルは特に問題ないと思われます。
最後に、構築したモデルで未知のデータを予測してみます。
pred = results.get_prediction(start=pd.to_datetime("1957-12-01"),
end = pd.to_datetime("1960-12-01"),
dynamic=False)
# 期待値と信頼区間を取り出す
pred_mean = pred.predicted_mean
pred_ci = pred.conf_int(alpha = .05)
# グラフの描画
data_2["1949-01-01":].plot(label="observed")
pred_mean.plot(label="forecast", alpha=.7, color = "r")
# 信頼区間の描画
plt.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='g', alpha=.2)
plt.xlabel("Date")
plt.ylabel("Passengers(log)")
plt.legend()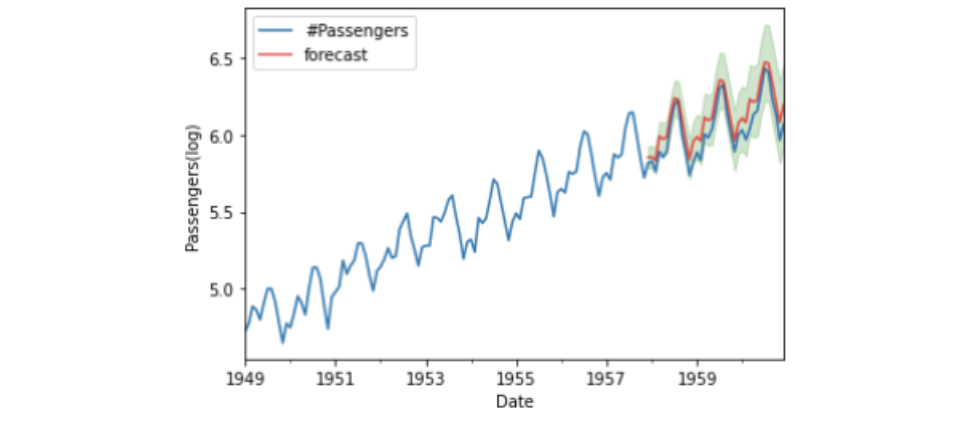
作成したSARIMAモデルで、乗客数をまずまずの精度で予測できていることが分かりました。
おわりに
非定常過程の説明に有効なARIMAモデルとSARIMAモデル、および、それらの基本となる定常過程に有効なMAモデル、ARモデル、ARMAモデルを見てきました。実際に得られるデータは非定常過程であることが多いので、ARIMAモデルとSARIMAモデルをマスターすることを目指してください。
参考サイト
Pythonによる時系列分析の基礎
PythonでのARIMAモデルを使った時系列データの予測の基礎[前編]
PythonでのARIMAモデルを使った時系列データの予測の基礎[後編]
未来を予測するビッグデータの解析手法と「SARIMAモデル」
https://deepage.net/bigdata/2016/10/22/bigdata-analytics.html#sarima%E3%83%A2%E3%83%87%E3%83%AB
定常時系列の解析に使われるARMAモデル・SARIMAモデルとは?
https://to-kei.net/time-series-analysis/sarima_model/
時系列分析の話~時系列モデル1~
https://masamunetogetoge.com/mamodel
時系列分析の話~時系列モデル2~
https://masamunetogetoge.com/armodel
A comprehensive beginner’s guide to create a Time Series Forecast (with Codes in Python and R)
piponではエンジニアの皆様に業務委託や副業でAI・データサイエンスの案件をご紹介しています!
piponの案件にご興味がある方は以下のフォームにご登録ください。案件をご案内します。


