1. はじめに
今回はPythonを使い、移動平均を算出する方法を紹介します。
移動平均とは、主に時系列のデータを平滑化するのによく用いられる手法で、株価のチャートで頻繁に見られるのでご存知の方も多いでしょう(「25日移動平均線」など)。データの長期的なトレンドを追いたいときに、よく用いられます。
2. 移動平均とは
「移動平均」と言ってもいくつかの種類、計算方法があるので、それぞれを見ていきましょう。
1) 単純移動平均(Simple Moving Average; SMA)
単純移動平均とは、直近の n 個のデータの単純な平均値を求めたものです。ある店舗のタピオカミルクティーの販売数の推移(表1)から、5日間の単純移動平均を求めてみましょう。
直近5日間の販売数の移動平均をYとすると、時点でのは、
Y=(Yt+Yt-1+Yt-2+Yt-3+Yt-4)/5
で求めることができます。式を見てわかる通り、直近と昔の販売数のデータが均等に織り込まれています。
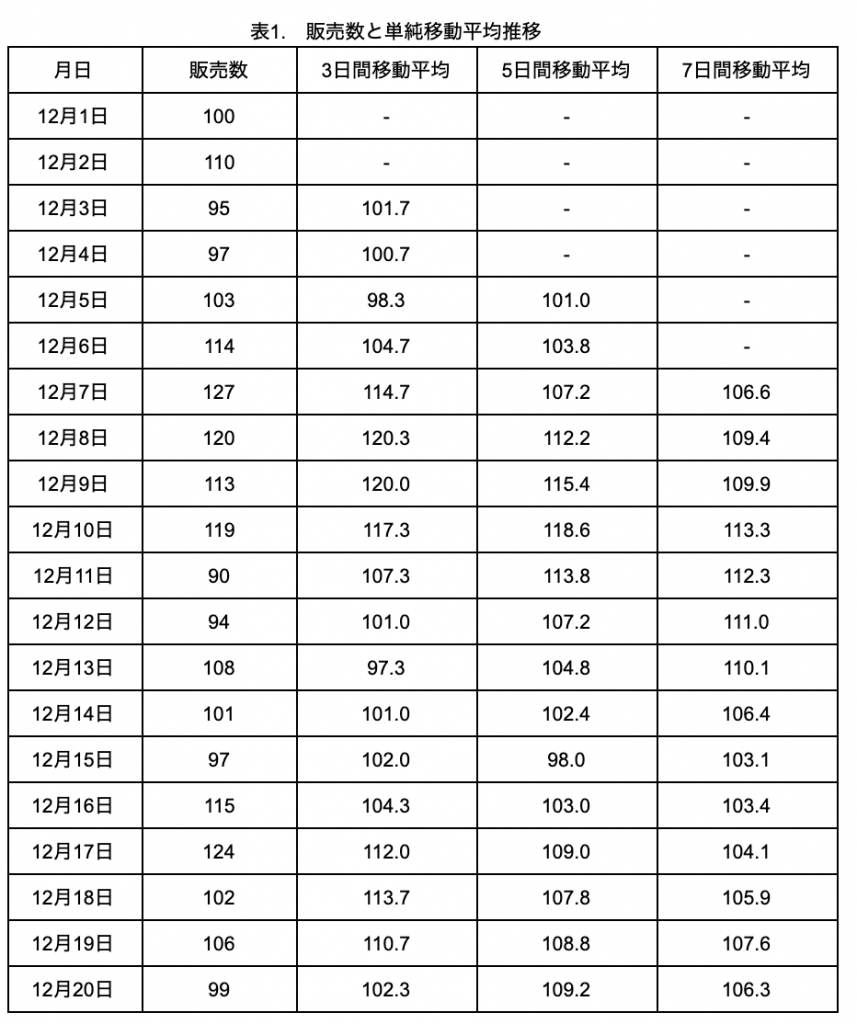
表1に3、5、7日間の移動平均を計算した列がありますが、Pythonでは以下のようにrollingメソッドを使うことで計算できます。
import pandas as pd
import matplotlib.pyplot as plt
#表の作成
data = {"月日":["2019-12-01","2019-12-02","2019-12-03","2019-12-04","2019-12-05",
"2019-12-06","2019-12-07","2019-12-08","2019-12-09","2019-12-10" ,
"2019-12-11","2019-12-12","2019-12-13","2019-12-14","2019-12-15",
"2019-12-16","2019-12-17","2019-12-18","2019-12-19","2019-12-20"],
"販売数":[100, 110, 95, 97, 103, 114, 127, 120, 113, 119, 90, 94, 108, 101, 97, 115, 124, 102, 106, 99]}
df = pd.DataFrame(data)
# 移動平均の計算
df["3日間移動平均"]=df["販売数"].rolling(3).mean().round(1)
df["5日間移動平均"]=df["販売数"].rolling(5).mean().round(1)
df["7日間移動平均"]=df["販売数"].rolling(7).mean().round(1)
print(df)月日 販売数 3日間移動平均 5日間移動平均 7日間移動平均
0 2019-12-01 100 NaN NaN NaN
1 2019-12-02 110 NaN NaN NaN
2 2019-12-03 95 101.7 NaN NaN
3 2019-12-04 97 100.7 NaN NaN
4 2019-12-05 103 98.3 101.0 NaN
5 2019-12-06 114 104.7 103.8 NaN
6 2019-12-07 127 114.7 107.2 106.6
7 2019-12-08 120 120.3 112.2 109.4
8 2019-12-09 113 120.0 115.4 109.9
9 2019-12-10 119 117.3 118.6 113.3
10 2019-12-11 90 107.3 113.8 112.3
11 2019-12-12 94 101.0 107.2 111.0
12 2019-12-13 108 97.3 104.8 110.1
13 2019-12-14 101 101.0 102.4 106.4
14 2019-12-15 97 102.0 98.0 103.1
15 2019-12-16 115 104.3 103.0 103.4
16 2019-12-17 124 112.0 109.0 104.1
17 2019-12-18 102 113.7 107.8 105.9
18 2019-12-19 106 110.7 108.8 107.6
19 2019-12-20 99 102.3 109.2 106.3はじめは、移動平均を計算できないためNANが入りますが、それぞれ3、5、7日目以降に計算値が入りきます。
これをグラフにすると、以下のようになります。
plt.plot(df["月日"], df["販売数"], label="daily")
plt.plot(df["月日"], df["3日間移動平均"], "k--", label="SMA(3)")
plt.plot(df["月日"], df["5日間移動平均"], "r--", label="SMA(5)")
plt.plot(df["月日"], df["7日間移動平均"], "g--", label="SMA(7)")
plt.xticks(rotation=90)
plt.xlabel("date")
plt.ylabel("quantity")
plt.legend()
plt.show()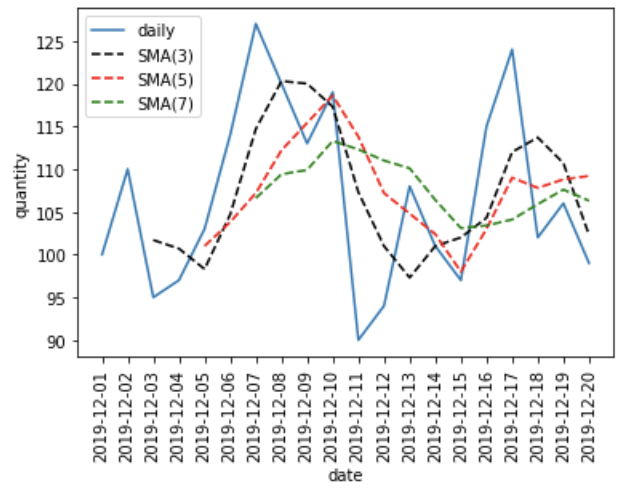
日々の販売量の推移に比べると、移動平均は平滑になっていることが分かります。そして、移動平均を算出する期間が長くなるほど、グラフは滑らかに推移することが分かります。移動平均を算出することで、推移のトレンドを見ることができます。
2) 加重移動平均(Weighted Moving Average; WMA)
指定期間のデータを単純に平均しただけの単純移動平均に対して、直近のデータに比重を置いた移動平均が、加重移動平均と指数移動平均です。
どちらも単純移動平均と比べてデータの変動に素早く反応するので、トレンドの変化を早めに捉えることができます。
直近の価格に徐々に比重を置いていく移動平均が、加重移動平均です。
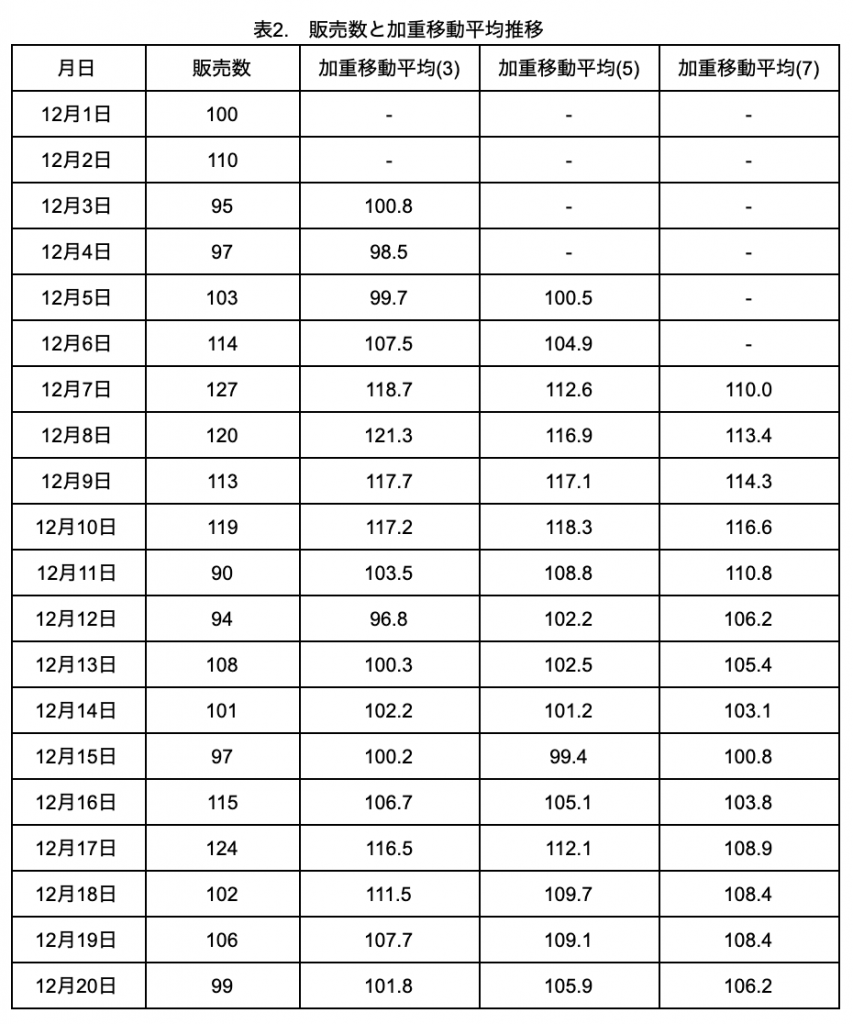
では、1)と同様に5日間の加重移動平均を求めてみましょう。
直近5日間の販売数の加重移動平均をYとすると、時点tでのYは、
Y=(5Yt+4Yt-1+3Yt-2+2Yt-3+1Yt-4)/(5+4+3+2+1)
で求めることができます。式を見てわかる通り、直近データに比重が置かれています。
表1の販売数のデータを使って求めた3、5、7日の加重移動平均を表2に示します。
Pythonには加重移動平均を求める関数はないため、自分で作る必要があります。
import pandas as pd
import matplotlib.pyplot as plt
#表の作成
data = {"月日":["2019-12-01","2019-12-02","2019-12-03","2019-12-04","2019-12-05",
"2019-12-06","2019-12-07","2019-12-08","2019-12-09","2019-12-10" ,
"2019-12-11","2019-12-12","2019-12-13","2019-12-14","2019-12-15",
"2019-12-16","2019-12-17","2019-12-18","2019-12-19","2019-12-20"],
"販売数":[100, 110, 95, 97, 103, 114, 127, 120, 113, 119, 90, 94, 108, 101, 97, 115, 124, 102, 106, 99]}
df = pd.DataFrame(data)
# 加重移動平均を求める関数
def wma(milktea):
weight = np.arange(len(milktea)) + 1
wma = np.sum(weight * milktea) / weight.sum()
return wma
df["加重移動平均(3)"]=df["販売数"].rolling(3).apply(wma, raw=True).round(1)
df["加重移動平均(5)"]=df["販売数"].rolling(5).apply(wma, raw=True).round(1)
df["加重移動平均(7)"]=df["販売数"].rolling(7).apply(wma, raw=True).round(1)
print(df) 月日 販売数 加重移動平均(3) 加重移動平均(5) 加重移動平均(7)
0 2019-12-01 100 NaN NaN NaN
1 2019-12-02 110 NaN NaN NaN
2 2019-12-03 95 100.8 NaN NaN
3 2019-12-04 97 98.5 NaN NaN
4 2019-12-05 103 99.7 100.5 NaN
5 2019-12-06 114 107.5 104.9 NaN
6 2019-12-07 127 118.7 112.6 110.0
7 2019-12-08 120 121.3 116.9 113.4
8 2019-12-09 113 117.7 117.1 114.3
9 2019-12-10 119 117.2 118.3 116.6
10 2019-12-11 90 103.5 108.8 110.8
11 2019-12-12 94 96.8 102.2 106.2
12 2019-12-13 108 100.3 102.5 105.4
13 2019-12-14 101 102.2 101.2 103.1
14 2019-12-15 97 100.2 99.4 100.8
15 2019-12-16 115 106.7 105.1 103.8
16 2019-12-17 124 116.5 112.1 108.9
17 2019-12-18 102 111.5 109.7 108.4
18 2019-12-19 106 107.7 109.1 108.4
19 2019-12-20 99 101.8 105.9 106.2これをグラフにすると、以下のようになります。
plt.plot(df["月日"], df["販売数"], label="daily")
plt.plot(df["月日"], df["加重移動平均(3)"], "k--", label="WMA(3)")
plt.plot(df["月日"], df["加重移動平均(5)"], "r--", label="WMA(5)")
plt.plot(df["月日"], df["加重移動平均(7)"], "g--", label="WMA(7)")
plt.xticks(rotation=90)
plt.xlabel("date")
plt.ylabel("quantity")
plt.legend()
plt.show()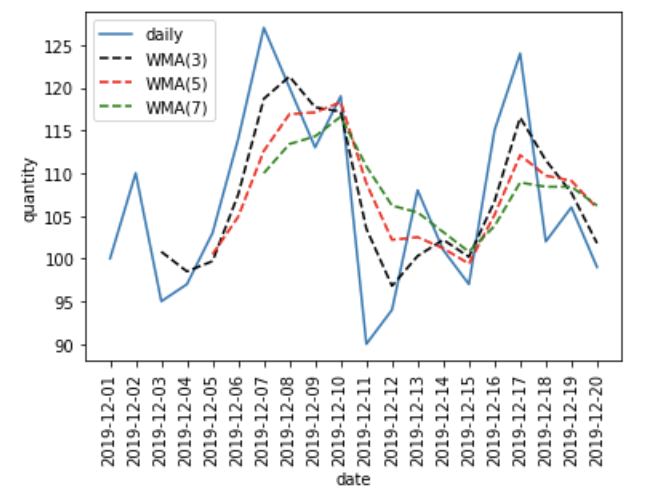
単純移動平均に比べると、販売数のデータの動きに近いことが分かります。これが、直近のデータに比重を置いた効果です。
3) 指数移動平均(Exponential Moving Average; EMA)
加重移動平均よりさらに直近のデータに比重を置き、過去の影響を指数関数的に重みを低くして算出する移動平均が、指数移動平均です。
比重の減少の程度は「平滑化係数」と呼ばれる、0と1の間の値を取る平滑定数αで決めます。
n日間の指数移動平均は、以下のように求められます
1日目:n日間の販売数の平均
2日目以降:前日の指数移動平均+平滑化定数α×{当日の販売数ー前日の指数移動平均}
ただし、α=2÷(n+1)
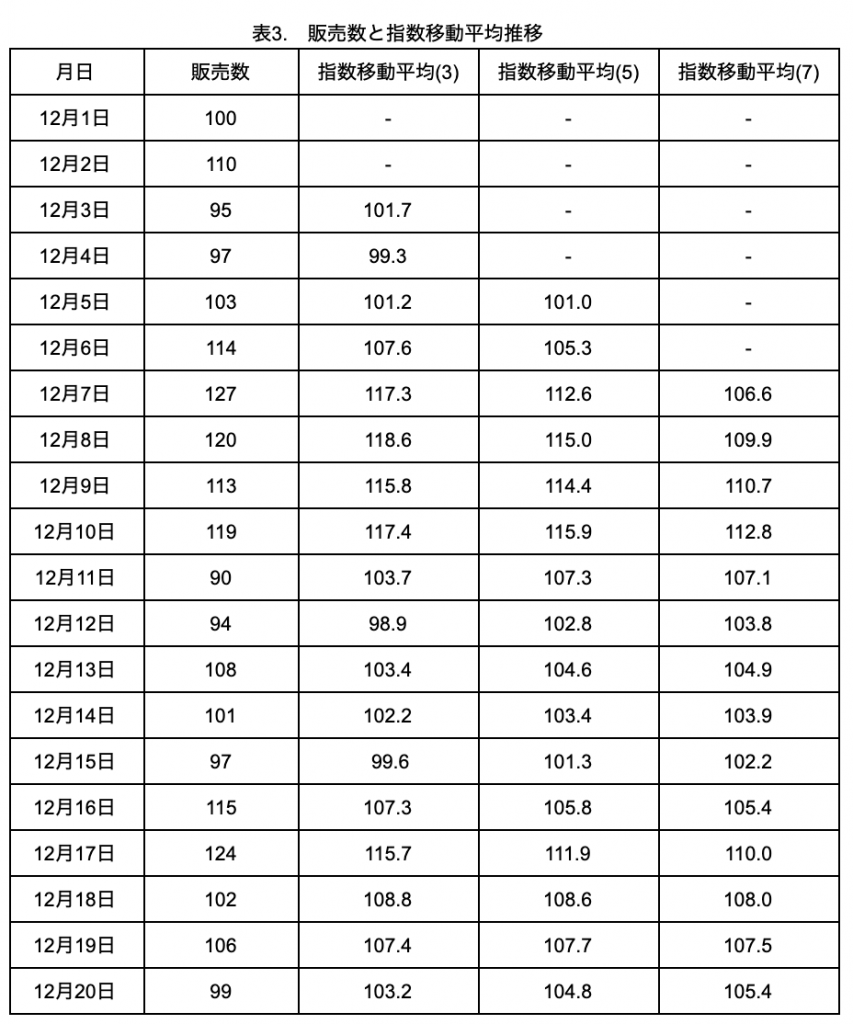
上記の計算式を用いて、表1の販売数のデータを使って求めた3、5、7日の指数移動平均を表3に示します。
表3. 販売数と指数移動平均推移
加重移動平均と同じく、Pythonには指数移動平均を求める関数はないため、自分で作る必要があります。
#表の作成
data = {"月日":["2019-12-01","2019-12-02","2019-12-03","2019-12-04","2019-12-05",
"2019-12-06","2019-12-07","2019-12-08","2019-12-09","2019-12-10" ,
"2019-12-11","2019-12-12","2019-12-13","2019-12-14","2019-12-15",
"2019-12-16","2019-12-17","2019-12-18","2019-12-19","2019-12-20"],
"販売数":[100, 110, 95, 97, 103, 114, 127, 120, 113, 119, 90, 94, 108, 101, 97, 115, 124, 102, 106, 99]}
df = pd.DataFrame(data)
# 指数移動平均を求める関数
def ema(milktea, period):
ema = np.zeros(len(milktea))
ema[:] = np.nan # NaN で一旦初期化
ema[period-1] = milktea[:period].mean() # 最初だけ単純移動平均で算出
for day in range(period, len(milktea)):
ema[day] = ema[day-1] + (milktea[day] - ema[day-1]) / (period + 1) * 2
return ema
df["指数移動平均(3)"]=ema(df["販売数"], 3).round(1)
df["指数移動平均(5)"]=ema(df["販売数"], 5).round(1)
df["指数移動平均(7)"]=ema(df["販売数"], 7).round(1)
print(df) 月日 販売数 指数移動平均(3) 指数移動平均(5) 指数移動平均(7)
0 2019-12-01 100 NaN NaN NaN
1 2019-12-02 110 NaN NaN NaN
2 2019-12-03 95 101.7 NaN NaN
3 2019-12-04 97 99.3 NaN NaN
4 2019-12-05 103 101.2 101.0 NaN
5 2019-12-06 114 107.6 105.3 NaN
6 2019-12-07 127 117.3 112.6 106.6
7 2019-12-08 120 118.6 115.0 109.9
8 2019-12-09 113 115.8 114.4 110.7
9 2019-12-10 119 117.4 115.9 112.8
10 2019-12-11 90 103.7 107.3 107.1
11 2019-12-12 94 98.9 102.8 103.8
12 2019-12-13 108 103.4 104.6 104.9
13 2019-12-14 101 102.2 103.4 103.9
14 2019-12-15 97 99.6 101.3 102.2
15 2019-12-16 115 107.3 105.8 105.4
16 2019-12-17 124 115.7 111.9 110.0
17 2019-12-18 102 108.8 108.6 108.0
18 2019-12-19 106 107.4 107.7 107.5
19 2019-12-20 99 103.2 104.8 105.4これをグラフにすると、以下のようになります。
plt.plot(df["月日"], df["販売数"], label="daily")
plt.plot(df["月日"], df["指数移動平均(3)"], "k--", label="EMA(3)")
plt.plot(df["月日"], df["指数移動平均(5)"], "r--", label="EMA(5)")
plt.plot(df["月日"], df["指数移動平均(7)"], "g--", label="EMA(7)")
plt.xticks(rotation=90)
plt.xlabel("date")
plt.ylabel("quantity")
plt.legend()
plt.show()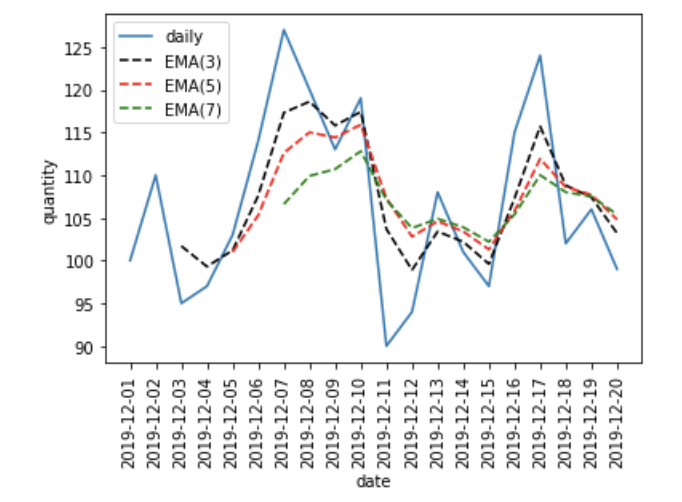
加重移動平均と同様に直近の値に比重を置いているため、トレンドは加重移動平均に近いものになります。
3. おわりに
時系列のデータ解析の際によく用いる、3種類の移動平均について見てきました。
Pythonでは単純移動平均は関数が用意されていますが、加重移動平均と指数移動平均は関数を自作する必要があります。
直近のデータに比重を置いている加重移動平均と指数移動平均は、単純移動平均と比べると元データの変化に素早く反応しますので、解析の目的に応じて使い分けるようにしましょう。
4. 参考サイト
移動平均の意味や目的、求め方、注意点
株価移動平均線の見方・使い方(1)~移動平均線の基礎
Pandas 演習としてのテクニカル指標計算 〜 移動平均の巻
加重移動平均線の見方・使い方
指数平滑移動平均線の見方・使い方
piponではエンジニアの皆様に業務委託や副業でAI・データサイエンスの案件をご紹介しています!
piponの案件にご興味がある方は以下のフォームにご登録ください。案件をご案内します。 https://share.hsforms.com/1qk0uPA_lSu-nUFIvih16CQegfgt

