機械学習の精度を上げたい時に使われるスタッキング(アンサンブル学習) を解説

この記事を書いた人

北爪聖也

株式会社pipon代表取締役。キャリアはADK(広告代理店)でテレビ広告運用をして残業120時間するが、ネット広告では自分の業務がAIで自動化されていることに驚愕する。そこで、機械学習受託会社に転職し、技術力を身につけた後、piponを創業。現在、製薬業界、大手監査法人、EC業界、様々な業界でAI受託開発事業を運営。

X Facebook YouTube

はじめに

今回は、「スタッキング」を紹介します。スタッキングとはアンサンブル学習の一つです。アンサンブル学習とは、一つの学習モデルをそのまま使うのではなく、複数の学習モデルを組み合わせることで、誤差を小さくする方法です。

アンサンブル学習には、複数の学習モデルの平均や多数決を取るvoting、作成済みの学習モデルの誤差を反映して、次の段の弱学習モデルを形成するboosting、そしてモデルを積み上げることで精度を上げるstacking(以下スタッキング)と呼ばれるものなどがあり、アンサンブル学習は機械学習の世界ではよく使われている手法です。

スタッキングの詳細

1)　スタッキングとは

スタッキングは非常に複雑になりがちな手法ですが、簡単な例として、二段階のモデルを考えましょう。
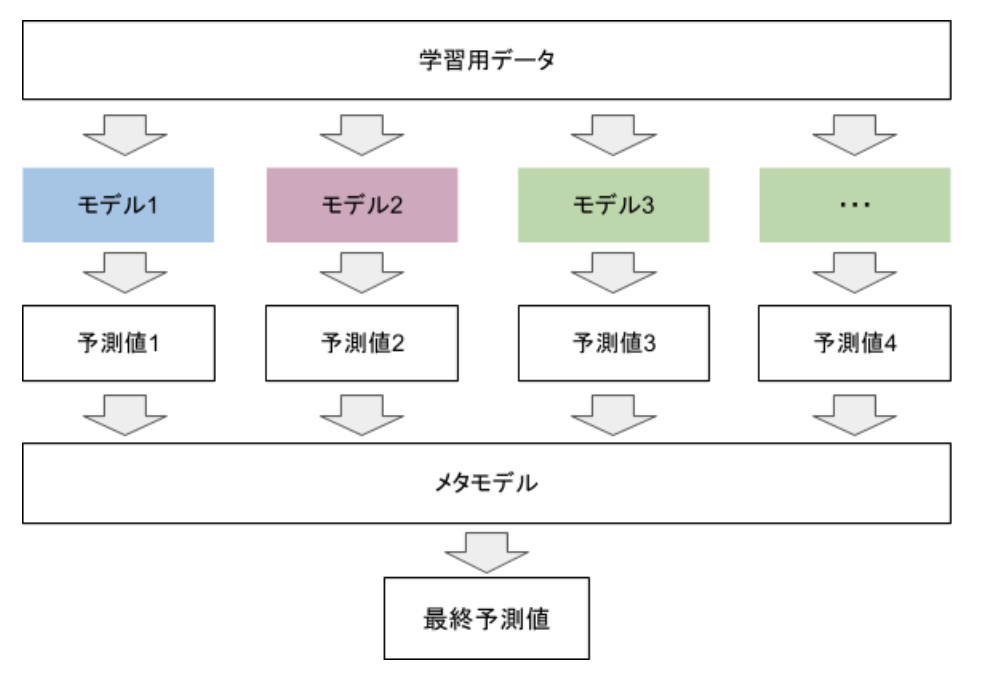
まず、第一段階で様々なアルゴリズム（ロジスティック回帰、ランダムフォレスト、ニューラルネットワークなど）にそれぞれ学習させ、予測値を出力します。第一段階の予測値を取りまとめるモデルを、メタモデルと言います。
そして、第一段階の各アルゴリズムの予測値を取りまとめたメタモデルは、第二段階で第一段階の予測値を特徴量として学習します。メタモデルで用いるアルゴリズムは特に決まりはありませんが、回帰モデルであれば、線形回帰モデルがよく使われます。正解率が高い学習モデルと低いモデルがあるので、より正解率の高い学習モデルを重視するなどの調整をして組み合わせることにより、ランダムで学習モデルを組み合わせるよりも精度が高くなることが期待できます。

2)　スタッキングの実装

それでは、Pythonを使ってスタッキングを行ってみましょう。今回は、スタッキングを紹介することが目的なので、予測精度を上げるための細かな調整は行っていません。

今回は、scikit-learnのbostonデータを使って、スタッキングを行います。まずは、データを読み込み、モデル作成と検証のためのデータセットを作ります。

import numpy as np
from sklearn.datasets import load_boston #Scikit-learnからbostonのデータをインポート
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from lightgbm import LGBMRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error

boston = load_boston() #データをbostonに代入

X, y = load_boston(return_X_y=True)

X_train_valid, X_test, y_train_valid, y_test = train_test_split(X, y, test_size=0.2, random_state=100)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_valid, y_train_valid, test_size=0.2, random_state=100)

print(X.shape, X_train.shape, X_valid.shape, X_test.shape)

(506, 13) (323, 13) (81, 13) (102, 13)

全データ506を、第1段階の学習用に323、メタモデル学習用に81、検証用に102に分けます。

今回は、線形回帰、ランダムフォレスト回帰、LightGBMの3つのアルゴリズムを使って行きます。まずは、それぞれを個別に使ってモデルを作ったときの性能を確認します。

# 第1段階のモデル作成

first_model_1 = LinearRegression() # 線形回帰
first_model_2 = RandomForestRegressor() # ランダムフォレスト回帰
first_model_3 = LGBMRegressor() # LightGBM 

first_model_1.fit(X_train, y_train)
first_model_2.fit(X_train, y_train)
first_model_3.fit(X_train, y_train)

# 結果の検証 
test_pred_1 = first_model_1.predict(X_test)
test_pred_2 = first_model_2.predict(X_test)
test_pred_3 = first_model_3.predict(X_test)

#　各モデル個別の予測精度を平均二乗誤差で確認
print ("モデル1の平均2乗誤差: {:.4f}".format(mean_squared_error(y_test, test_pred_1)))
print ("モデル2の平均2乗誤差: {:.4f}".format(mean_squared_error(y_test, test_pred_2)))
print ("モデル3の平均2乗誤差: {:.4f}".format(mean_squared_error(y_test, test_pred_3)))

モデル1の平均2乗誤差: 24.4851
モデル2の平均2乗誤差: 10.7506
モデル3の平均2乗誤差: 13.4078

平均二乗誤差で比べると、ランダムフォレスト回帰が最も精度よく予測できていました。

それでは、それぞれのモデルの出力を基に、スタッキングで予測してみましょう。

# スタッキングによる予測

# 第1段階の予測値(この後、メタモデルの入力に使用)
first_pred_1 = first_model_1.predict(X_valid)
first_pred_2 = first_model_2.predict(X_valid)
first_pred_3 = first_model_3.predict(X_valid)

#第1段階の予測値を積み重ねる
stack_pred = np.column_stack((first_pred_1, first_pred_2, first_pred_3))

# メタモデルの学習 
meta_model = LinearRegression()
meta_model.fit(stack_pred, y_valid)

# 各モデルの検証データを積み重ねる
stack_test_pred = np.column_stack((test_pred_1, test_pred_2, test_pred_3))

# スタッキングの検証
meta_test_pred = meta_model.predict(stack_test_pred)
print ("メタモデルの平均2乗誤差: {:.4f}".format(mean_squared_error(y_test, meta_test_pred)))

メタモデルの平均2乗誤差: 10.6040

今回のデータでは、線形回帰、ランダムフォレスト回帰、LightGBMを単体で用いるよりも、スタッキングの方が、わずかに誤差が小さいことが分かりました。