機械学習をやる上で線形代数はどのように必要になるのか

この記事を書いた人

北爪聖也

株式会社pipon代表取締役。キャリアはADK(広告代理店)でテレビ広告運用をして残業120時間するが、ネット広告では自分の業務がAIで自動化されていることに驚愕する。そこで、機械学習受託会社に転職し、技術力を身につけた後、piponを創業。現在、製薬業界、大手監査法人、EC業界、様々な業界でAI受託開発事業を運営。

X Facebook YouTube

はじめに

大学で学んだ線形代数は、様々な理論の基本となる考え方で、機械学習で用いられるアルゴリズムの中でも活用されています。
線形代数を知らなくても機械学習はできますが、なぜそのアルゴリズムで解を出せるのかを理解したい場合、線形代数の考え方を知っておく必要があります。
今回は、機械学習における線形代数の必要性について述べます。

線形代数とは

線形代数とは、線形空間に関する学問で、代数学の一分野です。簡単に言うと、行列やベクトルの性質を色々考える学問です。
理系の大学の授業では、1年次に必ず学習する科目の一つですが、ベクトルや行列など、高校数学では馴染みのない概念が色々出てきて、難解と感じる方も多いと思います。
しかし、様々なデータを解析するのに、高密度にデータを記述できるベクトルや行列の概念がとても重要になります。

では、まずは身近な例で線形代数を考えてみましょう。中学の時に学んだ連立方程式を思い出してください。

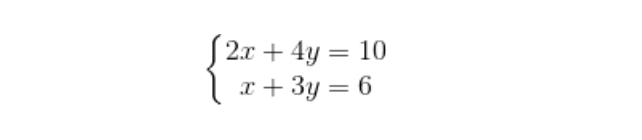
実は、連立方程式も線形代数の一つなのです。
例えば、上記のような2元1次方程式は、行列を使うと以下のように表せます。

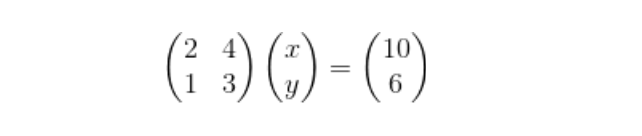
2元1次方程式であれば、わざわざ行列を使って表現するまでもありませんが、3元、4元・・・と多次元方程式になると、行列を使うことで高密度に表現することができます。線形代数とは、複雑な計算式を簡略化させたものと捉えていただいて構いません。

機械学習における線形代数の使われ方

では、線形代数が機械学習でどのように使われているかを見るため、シンプルな線形回帰モデルを考えてみます。統計学の世界では「重回帰分析」と言われている方法です。

表1はコンビニの売上高(目的変数)と、駅乗降客数、取扱い商品数などk個の特徴量のデータの例です。機械学習でやりたいことは、n個のデータを基に、k個の特徴量で売上高を精度よく予測するモデル(今回は、線形回帰モデル)を作ることです。

表1　店舗別売上データ

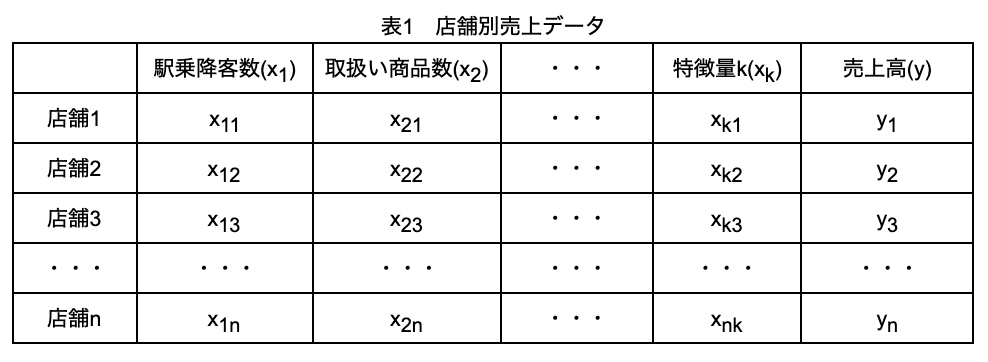
具体的には、求めたいモデル式は、y＝β0 + β1×1 + β2×2 + β3×3 + ・・・βkxkで、売上高を最も精度よく予測できる回帰係数β0、β1、β2、 β3 、・・・、βkを決める必要があります。

実際の機械学習では、例えばPythonであれば、scikit-learnのLinearRegressionモデルを使えば、行列のことを知らなくても簡単に求められるのですが、今回はその計算の仕組みを見てみましょう。

回帰係数β0、β1、β2、 β3 、・・・、βkが決まったとき、それぞれの店舗について、y＝β0 + β1×1 + β2×2 + β3×3 + ・・・βkxkという関係が、直接成り立っているわけではないことに注意してください。どの店舗についても、左辺と右辺がイコールになってくれれば理想ですが、実際はどうしても誤差が発生してしまいます。個々のデータについて、モデル式による予測値と実測値とのずれをεとすると、縦ベクトルを使うことで、以下のように表せます(式1)。

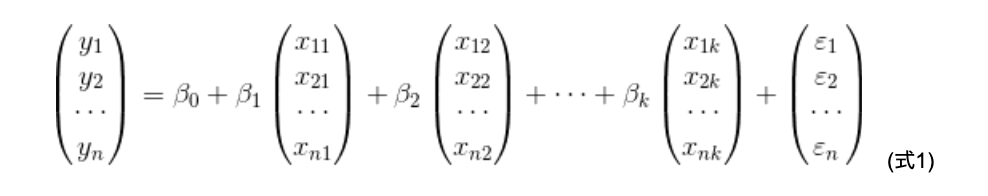
これを、簡略化して書くと、

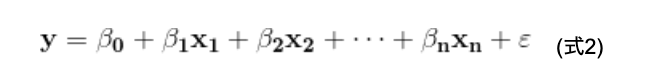
とコンパクトに書けます(式2)。
ここで説明変数は、データの件数n行分×特徴量の数k列分の、一つの行列Xでまとめることができます。

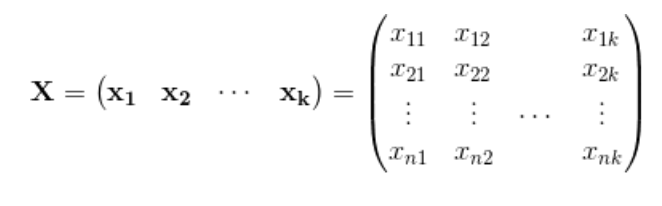
そして、

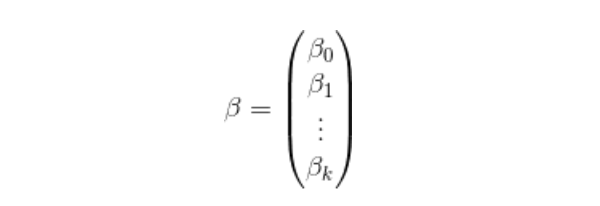
とすると、式2はさらに簡単に書き直すことができます(式3)。

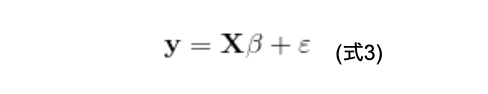
このように、行列を使うことで、式1が式3のようにとても簡単に書き直せます。
実際の線形回帰モデル(重回帰分析)では、式3から、

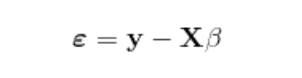
と変形し、

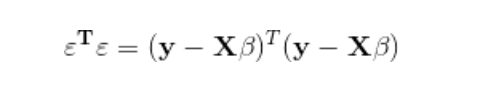
が最小となるように(最小2乗法)、ベクトルβで微分したものをゼロベクトルと置くことで、回帰係数βを求めることができます。なお、Tは転置行列を意味します。
詳細な回帰係数βの導出方法はここでは割愛しますが、線形回帰モデルを作るのに線形代数が重要な役割を果たしていることを理解してください。

さて、これまで線形回帰モデルは線形代数を使うと、簡単に記述できることを述べてきました。しかし、線形回帰モデルだけでなく、さらに複雑なアルゴリズムでも線形代数が有効なのです。

そこで、ニューラルネットワークの例を見てみましょう。
ニューラルネットワークとは、人間の脳神経系のニューロンを数理モデル化したものの組み合わせのことです。
もう少し具体的に書くと、出力層で望む結果（正解）が出るよう、パラメータ（重みとバイアス）を調整して予測モデルを作るアルゴリズムです。少し難しい言葉が出てきましたが、出力層を目的変数、パラメータを回帰係数と置き換えれば、線形回帰モデルとやっていることはほとんど同じであることが分かります。
従って、ニューラルネットワークも線形代数を用いることで、簡潔にモデルを書くことができるのです。
そこで、2層の単純なニューラルネットワークの例を見てみましょう(図1)

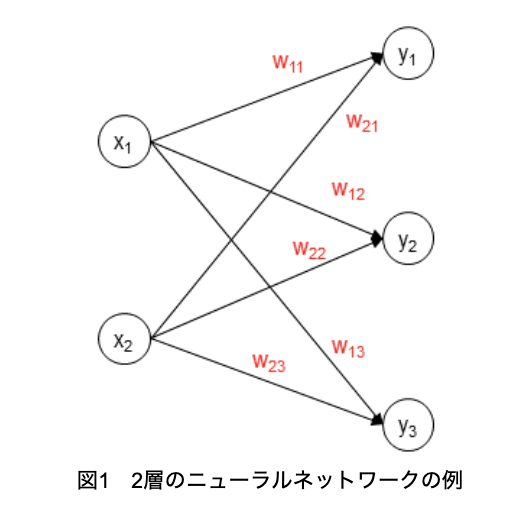
入力層である特徴量は、x1とx2の2つ、出力層はy1, y2, y3の3つです。入力層の値に重みw11～w23をかけてすべて加えることで、出力層の値が求まります。

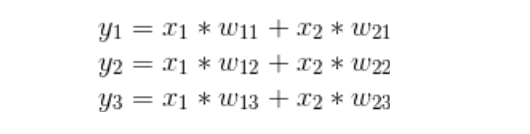
入力層が2つ、出力層が3つであれば、このように式を並べるのも苦ではありませんが、実際のデータのように特徴量やサンプル数が多くなると、とても書き表すことができません。
ここで、線形代数が威力を発揮するのです。

とおくと、

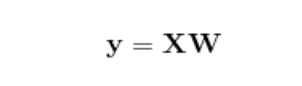
とシンプルに表すことができるのです。
実際は、ここから偏微分を行って最適モデルを作るのですが、今回は割愛します。
ここでは、ニューラルネットワークのような複雑なアルゴリズムでも、線形代数が基本となっていることだけ理解してください。

おわりに

今回は、機械学習において線形代数が必要となる理由を述べてきました。もちろん、線形代数を知らなくても、コンピュータが計算して最適モデルに導いてくれるので、機械学習を行うのに困ることはないかもしれません。
しかし、なぜそのモデルになるのか、とアルゴリズムを深く理解するためには、線形代数の知識が必須となるので、是非線形代数の知識を深めておいてください。