1. はじめに
今回は、「ロジスティック回帰」を紹介します。ロジスティック回帰とは、目的変数が二値変数である場合に、目的変数と特徴量の関係を検討したり、与えられた特徴量から未知の目的変数を予測したりするときに用いられるモデルです。
非常に分かりやすいシンプルなモデルで、解析結果は解釈しやすく、また、ニューラルネットワークの活性化関数にも関連するので、ここでロジスティック回帰をマスターしましょう。
2. ロジスティック回帰の詳細
1) ロジスティック回帰が適用できるデータの例
実例を使い、ロジスティック回帰の考え方を見ていきます。
温度と欠陥の有無(欠陥なし:0、欠陥あり:1)の関係を表すデータを、50個準備しました(図1)。ここでは特徴量は温度の1つのみですが、通常は複数個の特徴量を用いることが多いです。
import matplotlib.pyplot as plt
x = [128, 135, 126, 131, 126, 124, 133, 127, 129, 125,
128, 132, 125, 133, 128, 129, 130, 127, 125, 126,
133, 126, 125, 124, 131, 132, 128, 125, 135, 129,
133, 131, 127, 130, 127, 126, 125, 135, 131, 130,
125, 134, 134, 124, 128, 126, 124, 133, 134, 128]
y = [0, 1, 0, 0, 0, 0, 0, 0, 1, 0,
0, 1, 0, 1, 0, 1, 1, 0, 0, 0,
1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
1, 1, 0, 1, 0, 0, 0, 1, 1, 1,
1, 0, 1, 0, 1, 1, 0, 1, 1, 1]
plt.scatter(x, y)
plt.xlabel("Temperature", fontsize=14)
plt.ylabel("Defect", fontsize=14)
plt.tick_params(labelsize=14)
plt.show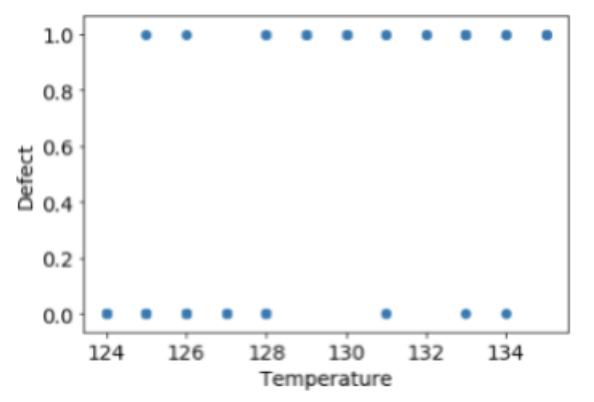
目的変数は0か1の二値となり、1つのプロットに複数のサンプルが重なっているので、分布の状況がよく分かりません。そこで、Pandasの濃淡散布図を使って表してみます(図2)。
import pandas as pd
df = pd.DataFrame(data={"Temperature":x, "Defect":y})
df.plot.hexbin(x="Temperature", y="Defect", gridsize=12, sharex=False)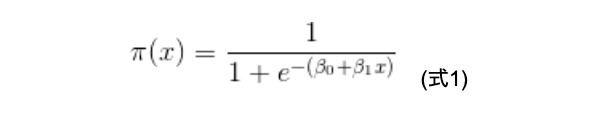
濃淡散布図では、濃い色ほど多くのサンプルが集まっていることを意味します。図2を見ると温度が低いときは欠陥が少なく、温度が高いと欠陥が増える傾向にあることが分かります。
さて、このようなデータが得られたときに、まず思いつく解析方法は線形回帰分析です。しかし、このような二値変数を目的変数とした場合、得られた回帰式で未知のデータを予測すると、0を大きく下回るあるいは、1を大きく上回ってしまう、といったことが起こることがあります。そこで、最小値が0、最大値が1となるような回帰モデルが求められ、それを実現するモデルがロジスティック回帰モデルです。
2) ロジスティック回帰の考え方
次に、ロジスティック回帰の考え方を少し詳しく見ていきましょう。
最小値が0、最大値が1となる回帰モデルとして、式1で表されるロジスティック曲線を想定しましょう。
式1において、β0=-5、β1=0.5として、xとπ(x)の関係を示したグラフを図3に示します。
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(0., 20., 0.001)
y = 1 / (1+np.exp(-(-5+0.5*x)))
plt.plot(x, y)
plt.axhline(0, linewidth = 1, ls = "-", color = "black")
plt.axhline(1, linewidth = 1, ls = "-", color = "black")
plt.xlabel("x", fontsize=14)
plt.ylabel("π(x)", fontsize=14)
plt.tick_params(labelsize=14)
plt.show()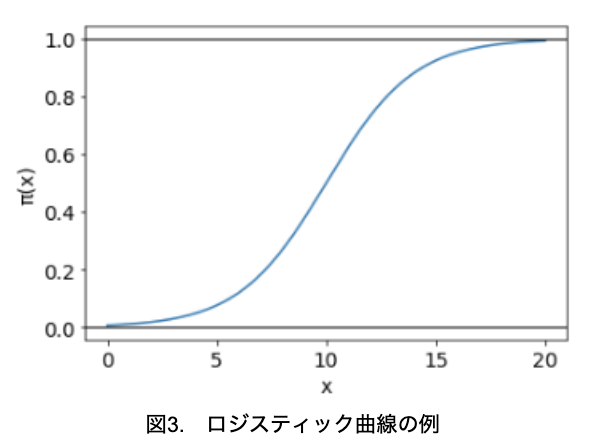
曲線はS字型となっており、π(x)は0~1の値になっていることが分かります。このような関数を、シグモイド関数とも呼びます。
また、π(x)=0.5付近では直線的に変化し、π(x)が0または1に近いときは、その傾きが緩やかになっています。
式1の両辺の自然対数を取って変形することで、式2が得られます。
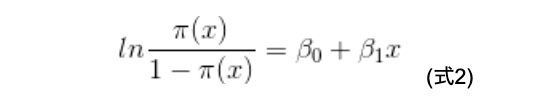
式2の右辺はxの1次式となっているので、横軸にx、縦軸にln((x)/(1-(x))取ってプロットすると、図4のように直線となります。
余談ですが、シグモイド関数はニューラルネットワークの活性化関数として利用されることもあります。
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(0., 20., 0.001)
y = -5+0.5*x
plt.plot(x, y)
plt.xlabel("x", fontsize=14)
plt.ylabel("ln(π(x)/(1-π(x))", fontsize=14)
plt.tick_params(labelsize=14)
plt.axhline(0, linewidth = 1.5, ls = "-", color = "black")
plt.grid(True)
plt.show()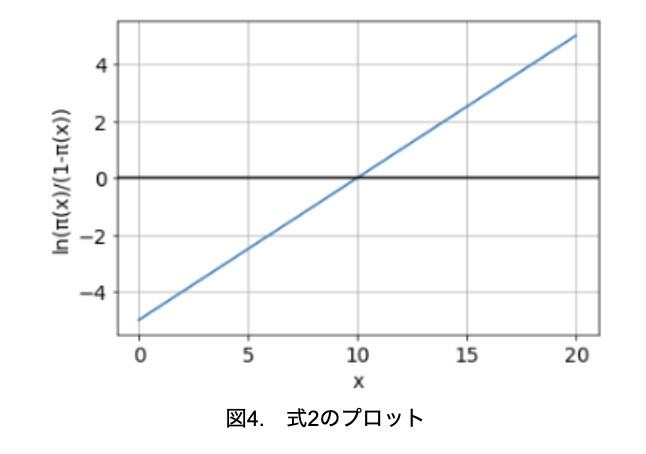
さて、ロジスティック曲線を考えることで、最終的に図4のように直線の関係に持ち込むことができました。あとは、通常の線形回帰でパラメータβ0、β1を求めればよいのではと思われるかもしれませんが、実はそういうわけにはいきません。
線形回帰では最小2乗法によりβ0とβ1を推定できますが、その前提として誤差項に対して、期待値0の不偏性、目的変数の分散と同じである等分散性を仮定しています。目的変数が数値データであれば、通常この前提条件は満足しますが、目的変数が二値変数の場合、等分散性を仮定することができません。
そこで、ロジスティック回帰ではβ0とβ1の推定方法として、最小2乗法ではなく最尤法という方法が用いられます。
最尤法とは、観測されたデータの得られる確率が最大となるように、パラメータを推定する方法です。
最尤法によるパラメータの推定は多くの計算が必要となり、またその理論をここで述べるにはあまりに難しい内容であるため、ここでは割愛します。通常は、ニュートンラフソン法、準ニュートン法、反復重み付き最小2乗法のいずれかが用いられるので、興味がある方は調べてみてください。
さて、最尤法でパラメータを推定することで、回帰式が得られますので、その回帰式でサンプルが特定のクラスに属している確率を予測し、確率の大きいクラスに分類することができます。
3) ロジスティック回帰の具体例
それでは、Pythonのscikit-learnで用意されているcancerデータを使って、実際に決定木分析を行ってみましょう。
cancerデータとは、乳がんの検査で採取した細胞のデジタル画像から、30の特徴量を抽出し、それぞれのサンプルに対して、良性腫瘍か悪性腫瘍の診断結果が付けられている分類データです。
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
#データの読み込み
cancer = load_breast_cancer()
#学習用データとテスト用データに分割
X_train, X_test, Y_train, Y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=10)
# ロジスティック回帰
clf = LogisticRegression(max_iter=10000, random_state=10)
clf.fit(X_train, Y_train)
#結果
print("学習用データの精度:{:.3f}".format(clf.score(X_train, Y_train)))
print("テスト用データの精度:{:.3f}".format(clf.score(X_test, Y_test)))学習用データの精度:0.967
テスト用データの精度:0.944
PythonのLogisticRegression関数では、最適化は準ニュートン法の一つである、L-BFGS法(範囲制約付きメモリ制限BFGS法)がデフォルトとなっています。
また、最適化の反復回数はデフォルトでは最大100回ですが、今回の場合は収束しなかったので、最大を10000回で解析しています。
さて次に、どの特徴量がどのように予測に寄与しているか見てみましょう。
import pandas as pd
#回帰係数を分かりやすいように表にする
coef = pd.DataFrame(clf.coef_.reshape((30, -1)), cancer.feature_names, columns=["回帰係数"])
interce = pd.DataFrame([clf.intercept_], index=["定数項"], columns=["回帰係数"])
df_coef = pd.concat([coef, interce])
df_coef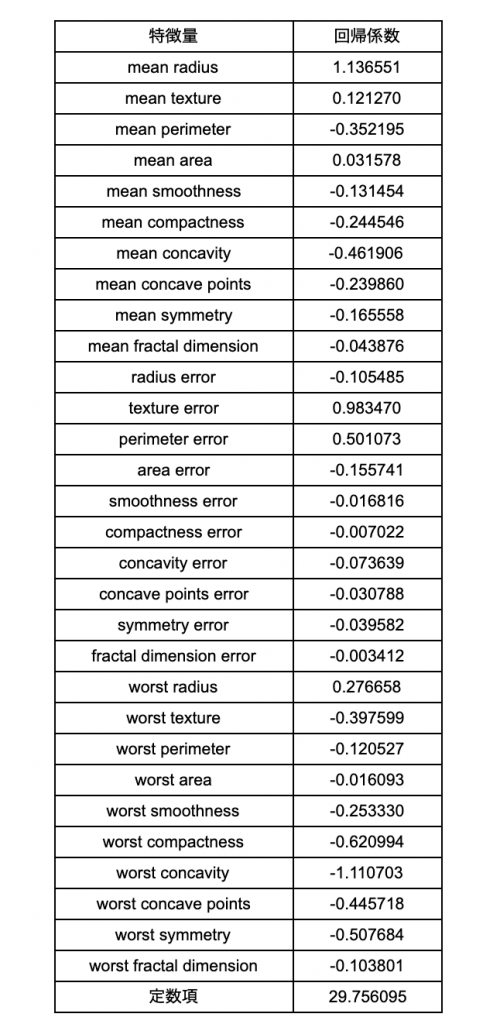
回帰係数が正の場合、その特徴量が増えれば、結果はプラスつまり、良性方向に向かいます。そして回帰係数が負の場合は、その逆になります。
上記の解析結果の場合、mean radiusが増えると良性の傾向になり、mean perimeter増えると悪性の傾向になります。
このように、ロジスティック回帰は分析結果を詳細に検討できるので、従来の知見との比較や、プラス方向に持っていくにはどうすればよいかなど、次のアクションに向けた考察が可能となります。
3. おわりに
今回はロジスティック回帰を見てきました。特徴は以下になります。
①ロジスティック回帰は、分析結果の解釈がしやすいメリットがあります。
②また、2値分類データに適用する際に適しているアルゴリズムです。
この2つが、マーケティングデータの解析で多用される理由です。マーケティングでは購買情報(買ったか買わなかったの2値分類)や広告のクリック情報(クリックしたかしてないかの2値分類)というように、2値分類をしたいシーンが多くあります。
また、購買情報や広告クリックがどういう要因で起こったのかを知って、またマーケティング活動へフィードバックします。
購買に効いているデータを解析して、「恵比寿に住んでいる20代女性で、彼女たちは、渋谷に住んでいる20代女性より2倍も購入しやすい」ということがわかったら、自分たちの商品を愛してくれている顧客像がはっきりしてきます。
是非、マーケティングデータの解析でロジスティック回帰使って頂けると嬉しいです!
4. 参考サイト
初めてのロジスティック回帰
PRML4.3.3
ロジスティック回帰を最急降下法とニュートン法で解く
ロジスティック回帰(教師有り学習)
piponではエンジニアの皆様に業務委託や副業でAI・データサイエンスの案件をご紹介しています!
piponの案件にご興味がある方は以下のフォームにご登録ください。案件をご案内します。


