はじめに
今回は、状態空間モデルを紹介します。状態空間モデルとは、実際の状態を表す変数と実際に観測できる変数が異なるような系を数式で表現したもので、気象の予測や制御理論など様々な分野で応用することができます。
状態空間モデルはデータサイエンスの世界でも用いられており、時系列データの解析でもよく使われている考え方です。古典的な時系列解析モデルとして、MAモデル、ARモデル、ARMAモデル、ARIMAモデルがよく知られていますが、これらのモデルでカバーできない時系列データに対して、状態空間モデルは威力を発揮します。その状態空間モデルを見ていきましょう。
古典的な時系列解析モデルの限界
古典的な時系列解析モデルは、観測した時系列データからパターンを見つけ出し、それを単純な数式に置き換える考え方で、将来の予測によく使われます。例えば、これまでの売上実績をもとに、将来の売上を予測するような場合です。
古典的な時系列解析モデルでも、十分実用に耐えうる予測は可能ですが、適用できない場面もあります。
時系列解析モデルは、1時点前のデータを使って予測モデルを作るため、トラブルなどでデータが欠けてしまった場合は、その後の予測は不可能になるのです。
1時点前のデータがなくてもその後のデータを予測したいことは、実務ではよくあることですが、古典的な時系列解析モデルでは、何ともなりません。このようなときに、将来を予測してくれるモデルが、状態空間モデルなのです。
他にも、古典的な時系列解析モデルでは次数を固定する必要がある、という制約もあります。次数を固定するということは、データの周期を固定することを意味しており、実務で得られるデータに対しては、適用が難しい面があります。
これについても、状態空間モデルであれば、柔軟に予測モデルを作ることができるので、汎用性が高いモデルと言えるでしょう。
状態空間モデルとは
状態空間モデルを模式図で表すと、図1のようになります。状態空間モデルは、観測できない「状態モデル」(例えば市況や体調)と観測した結果である「観測モデル」(例えば株価や体温)からなります。
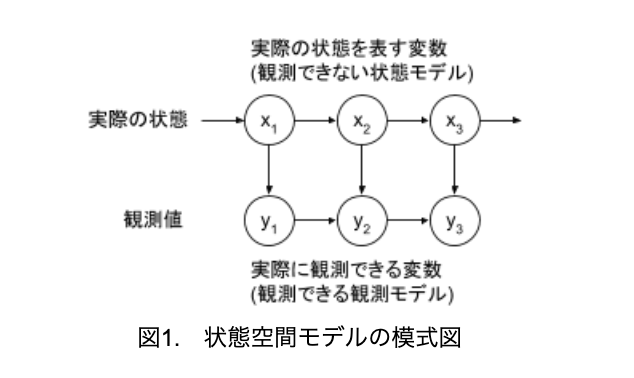
分かりにくいので、簡単な例で考えてみます。
体調管理のため、毎朝体温を測定しているとしましょう。体温は一定であることはなく、高い時もあれば低い時もあります。体温の変化の理由は何でしょうか?体調が悪くて体温が変化する可能性もあれば、体調は問題ないものの何らかの誤差により変化する可能性もあります。
つまり、図1の、状態が変化したから観測値も変化したのか、状態は変化していないものの観測値が変化したのか、ということになります。
これを、以下のように数式で表すことができます。
xtを状態変数(実際の状態を表す変数、ytを実際に観測できるデータとすると、
・観測モデル:yt=gt(xt, wt)
・状態モデル:xt+1=ft(xt, vt)
観測データ ytは、同時点の観測できない状態xtと観測ノイズwtの関数で表されます。xt+1は1時点前の状態 xt+1と状態ノイズvtの関数で表されます。状態ノイズは、上昇傾向や下降傾向といったトレンドなど、状態そのものの変化と考えてください。古典的な時系列解析モデルでは、「観測値」のみを取り扱っていますが、状態空間モデルでは、「状態」と「観測値」の二つに分けて考え、得られた観測値から見えない状態を推定することになります。
状態空間モデルのメリットは、モデリングの柔軟性が高いことと、観測値の増減要因を説明できることです。
Pythonによる状態空間モデルの構築例
では、Pythonを使って状態空間モデルを作成してみます。Rの時系列データ解析の例でよく用いられるAirPassengersのデータを使って、状態空間モデルで実際に解析してみます。
それでは、AirPassengersのデータを読み込んで、生データを見てみましょう。
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv("AirPassengers.csv",
index_col="Month",
parse_dates=True,
dtype="float")
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.plot(data["#Passengers"])
ax1.set_title("Passengers trend")
ax1.set_xlabel("Year")
ax1.set_ylabel("Passengers")
plt.show()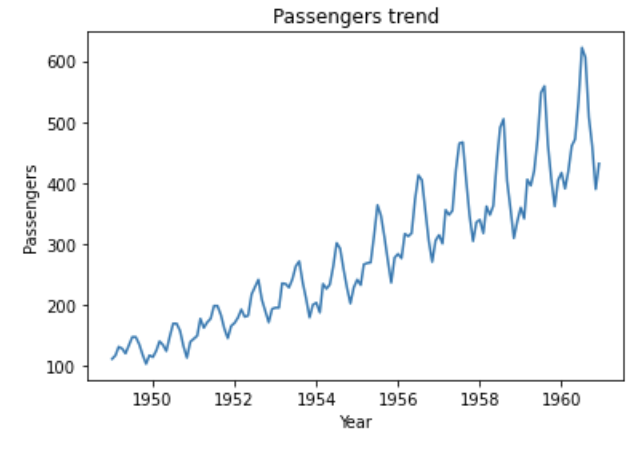
右上がりの上昇傾向が見られるとともに、季節要因と思われる周期的な変動が見られます。古典的な時系列解析ではSARIMAモデルで解析できるこの事例を、状態空間モデルで解析してみます。
状態空間モデルを作る際にやっていることは、
1.1期前の状態推定値を使って、次の状態を予測する
2.予測された状態推定値を、当期のデータを使って修正する→これをフィルタリングと言います
の2ステップですが、2ステップ目のフィルタリングで用いられる方法の1つが、カルマンフィルタです。以下の例では、カルマンフィルタを用いて予測する例です。
#季節変動ありの線形トレンドモデル
import statsmodels.api as sm
season_trend = sm.tsa.UnobservedComponents(
data,
level='local linear trend',
seasonal=12)
keisan_season_trend = season_trend.fit() #カルマンフィルタで最適化
# 推定結果をプロット
kekka = keisan_season_trend.plot_components(figsize=(12, 18))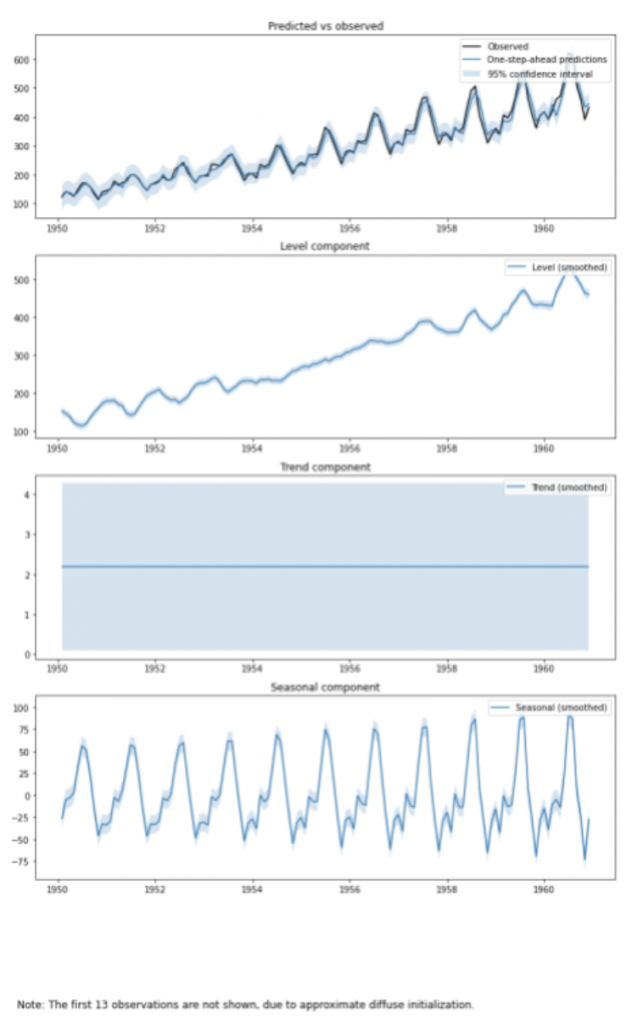
1つ目のグラフは、観測値と予測値とその95%信頼区間です。2つ目のグラフは、観測できない状態を表すグラフです。3つ目のグラフは、トレンドのグラフです。ここではほぼフラットになっており、同じペースで乗客が増加していることが推測できます。4つ目のグラフは、季節成分のグラフです。乗客数が周期的に変化していることが分かります。
状態空間モデルは、得られた観測値から様々な成分に分けて解釈することができるため、次のアクションにつなげやすいというメリットがあります。
では、最後に作成したモデルで将来を予測してみます。
# 将来の予測
prediction = keisan_season_trend.predict('1959-01-01', '1962-12-01')
# 観測値と予測値のプロット
plt.plot(data)
plt.plot(prediction, color="red")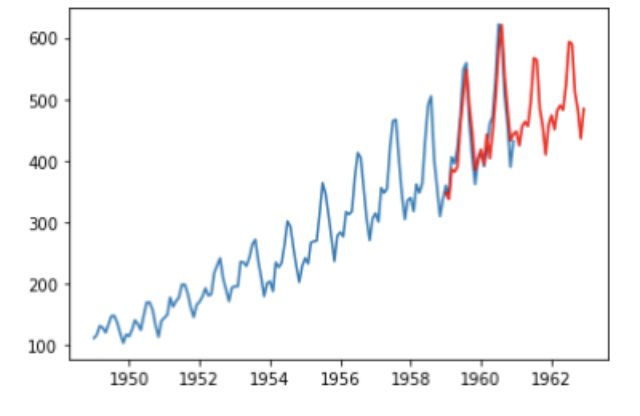
今回は季節成分ありのローカル線形トレンドモデルを構築して予測に用いましたが、その他のモデルもあるので、実際の解析ではいくつかのモデルを試して、最も精度よく予測できるモデルを選ぶとよいでしょう。
3. おわりに
今回は、時系列データの解析に有効な状態空間モデルを見てきました。状態モデルと観測モデルを考えることが大きな特徴で、時系列データの解析ではよく使われるモデルの1つです。時系列データを解析する際は、是非トライしてみてください。
参考サイト
状態空間モデル
状態空間モデルとは
時系列データ解析における状態空間モデルの枠組み
https://to-kei.net/time-series-analysis/state_space_model/
なぜ状態空間モデルを使うのか
Pythonで状態空間モデルを使う(StatsModels)
状態空間モデルの推定方法の分類
piponではエンジニアの皆様に業務委託や副業でAI・データサイエンスの案件をご紹介しています!
piponの案件にご興味がある方は以下のフォームにご登録ください。案件をご案内します。 https://share.hsforms.com/1qk0uPA_lSu-nUFIvih16CQegfgt


