時系列解析における定常過程について解説

この記事を書いた人

北爪聖也

株式会社pipon代表取締役。キャリアはADK(広告代理店)でテレビ広告運用をして残業120時間するが、ネット広告では自分の業務がAIで自動化されていることに驚愕する。そこで、機械学習受託会社に転職し、技術力を身につけた後、piponを創業。現在、製薬業界、大手監査法人、EC業界、様々な業界でAI受託開発事業を運営。

X Facebook YouTube

はじめに

今回は、時系列解析における「定常過程」を見ていきます。解析対象となる時系列データとは、時間の推移とともに特定の時間間隔で観測されるデータのことで、観測される順序に意味があります。例えば、ある都市の1時間ごとの気温を記録したものや、株価の終値を毎日記録したものなどが、時系列データに該当します。

そして、時系列データの解析の中で重要な概念が「定常性」と「自己相関」です。今回は特に、定常性に焦点を当てていきます。

定常過程の詳細

1)　時系列データの性質

定常性を考えるにあたり、確率変数列{R₁, R₂, R₃, …, R_n}とそこからの実現値{r₁, r₂, r₃, …, r_n}を定義します。なお、確率変数とは、どのような値になるのか確率が定まっている性質を持つ変数を指します。さて、添え字の1～nを順序関係の意味を持たせた時刻とすれば、{r₁, r₂, r₃, …, r_n}は時系列データとみなせます。従って、時系列解析とは観測されたr_tを基に、その母集団に相当するR_tを推測することと言えます。

では、R_tの平均と分散を考えてみましょう。時点tの確率変数R_tに関する平均をE(R_t)とすると、異なる時点の平均E(R₁), E(R₂), ・・・, E(R_t)が等しいという前提は置いていないため、E(R_t)の推定値として、標本平均(r₁, r₂, ・・・, r_nの平均)を使うことはできません。なぜなら、R₁, R₂, R₃の平均が異なる場合もあり得るからです。確率変数R_tの分散(ばらつき)Var(R_t)も同じく、R₁, R₂, R₃の分散が異なる場合があるため、標本分散(r₁, r₂, ・・・, r_nの分散)を使うことはできません。

そもそも、確率変数列{R₁, R₂, R₃, …, R_n}が同じ分布に従うと仮定していないため、それぞれの時点で確率変数が従う分布は異なることもあり得ます。この状態のイメージを表すと、図1のようになります。

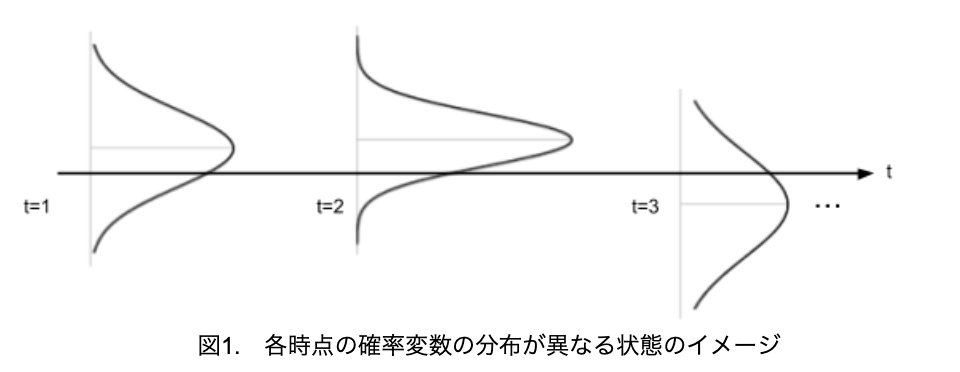
各時点での確率変数を精度よく推定しようと思ったら、ある時点tにおいてサンプルをたくさん採取する必要がありますが、時系列データでは各時点の観測値は1つであり、各時点でのサンプル数を増やすことは不可能です。

2)　定常性とは

そこで、時系列解析を行うにあたり、確率変数列{R₁, R₂, R₃, …, R_n}に対して前提条件を決めてあげる必要があります。通常、時系列解析では、時点tに依存せず、①平均E(R_t)は一定、②分散Var(R_t)は一定、③自己共分散Cov(R_t, R_t-h)はラグhのみに依存、を前提とします。ここでラグとは、時点のずらし量のことです。確率変数列{R₁, R₂, R₃, …, R_n}が①～③の3条件を満たすとき、定常性を持つと定義します。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

3)　定常過程とは

上述のとおり、時系列解析では、時系列データ{r₁, r₂, r₃, …, r_n}をある確率変数列{R₁, R₂, R₃, …, R_n}からの1つの実現値とみなしますが、この確率変数列のことを確率過程と言い、定常性を持つ確率過程のことを「定常過程」と呼びます。

定常性の定義より、定常過程はトレンドを持たず、また、平均回帰的であることが大きな特徴です。平均回帰的とは、データが平均の方向に戻っていく傾向のことです。

定常過程のデータ例

それでは、実際の時系列データを使って、定常過程とは何かを見てみましょう。データは、2018年から2019年の日経平均株価の終値とします。

日経平均株価のデータは、このサイトからダウンロードできます(表1)。

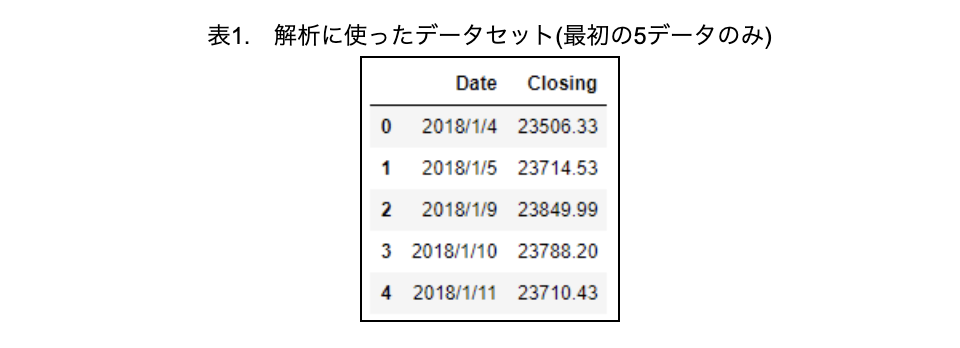
まずは、生データをプロットしてみましょう(図1)。

import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv("日経平均株価.csv", header=0)

fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.plot(data["Date"], data["Closing"])
ticks = 30
ax1.set_xticks(range(0, 501, ticks))
ax1.set_xticklabels(data["Date"][::ticks], rotation=90)

ax1.set_title("日経平均株価推移")
ax1.set_xlabel("年月日")
ax1.set_ylabel("株価(円)")

plt.show()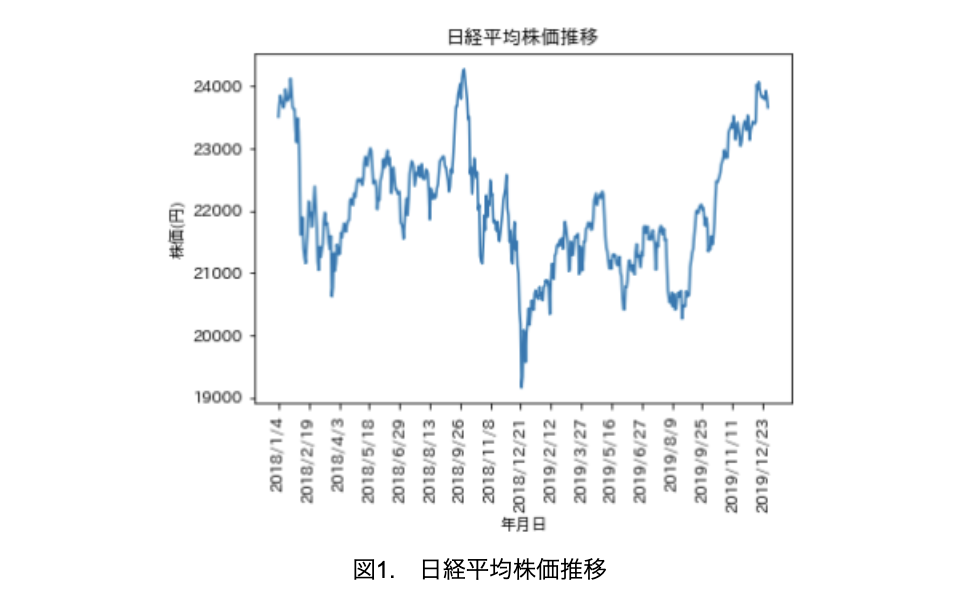

各時点において、確率変数列の平均が同じであることが、定常性であるためには必要な条件ですが、とてもそのように見えないことが分かります。この状態を、非定常過程と言います。そこで、株価の対数を取り、ある時点とその次の時点の対数差分を計算して(表2)、それをプロットしてみましょう(図2)。

import numpy as np

data2 = data["Closing"].to_numpy()
data2 = np.log10(data2)
data3 = np.diff(data2, n= 1)
data3 = np.insert(data3, 0, np.nan)

data["Closing_diff"] = data3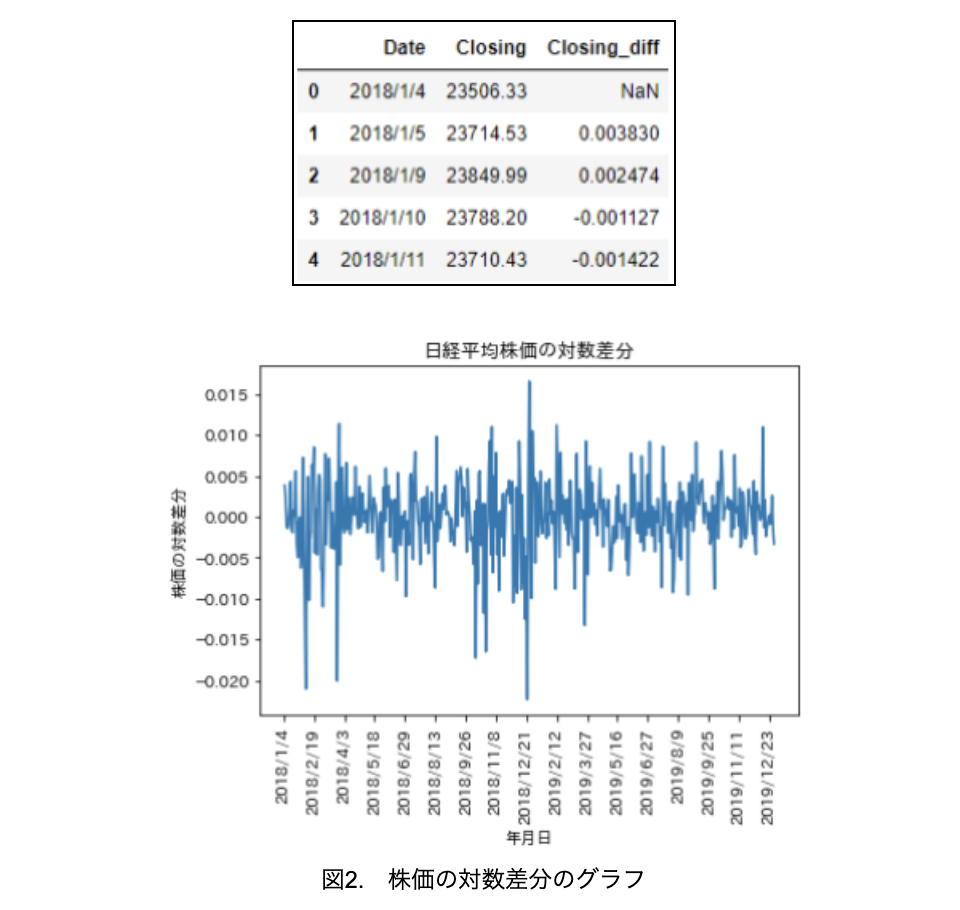

株価の対数を取って、前日との差分をプロットすると、0付近を中心にプラス側とマイナス側へ同程度にばらついていることが分かります。特にトレンドはなく、0に戻ってくる傾向があることから、対数差分は定常過程と推測できます。

統計的に判断するためには、単位根検定で確認することができます。単位根検定には何種類かありますが、今回はADF検定という方法で検定してみます。

ここで、単位根過程とは、原系列r_tが非定常過程で、差分系列Δr_t=r_t−r_t−1が定常過程である過程のことを指します。

ADF検定は、単位根であることを帰無仮説として検定するので、帰無仮説が棄却されなければ、差分は定常過程とみなせるということです。

では、株価のADF検定を行ってみましょう。


import statsmodels.api as sm

# 単位根検定
adf_result = sm.tsa.stattools.adfuller(data["Closing"])
adf_result

(-2.5459183364625035,
 0.10469776192030666,
 0,
 485,
 {'1%': -3.443905150512834,
  '5%': -2.867517732199813,
  '10%': -2.569953900520778},
 6402.627752259782)

検定統計量は-2.55でp値は0.105で5%有意とはならず、有意水準5%で帰無仮説は棄却されませんでした。従って、元データは非定常過程、差分データは定常過程であるとみなせることが、統計的に言えたので、表2のデータは定常過程を前提とした手法を用いて、時系列解析が可能であることが分かりました。