データサイエンスにとっての正規分布の重要性とは何か？

この記事を書いた人

北爪聖也

株式会社pipon代表取締役。キャリアはADK(広告代理店)でテレビ広告運用をして残業120時間するが、ネット広告では自分の業務がAIで自動化されていることに驚愕する。そこで、機械学習受託会社に転職し、技術力を身につけた後、piponを創業。現在、製薬業界、大手監査法人、EC業界、様々な業界でAI受託開発事業を運営。

X Facebook YouTube

はじめに

今回は、正規分布のお話をしたいと思います。正規分布と言えば、統計学の世界でよく聞かれますが、データサイエンスの世界でも、やはり重要な考え方です。

ここでは、正規分布の考え方や性質を見ていきますので、これらをデータサイエンスの中でうまく活用してください。

正規分布の詳細

1)　正規分布とは

正規分布の考え方は、我々の生活の中でも使われています。例えば、学生時代に頭を悩ませた「偏差値」も、実は正規分布の考え方に基づいて計算されています。

それでは、統計学の考え方に基づき、正規分布の考え方を見ていきます。

あなたは、金属の棒を生産していると仮定しましょう。棒の長さを保証する必要があるため、サンプルを抜き取って、検査工程で長さを測定しています。

このとき、長さの測定値はどの棒もすべて全く同じになるでしょうか？答えはNoです。長さのばらつきを抑えようと、どんなに製造条件を厳密に管理しても、多かれ少なかれ測定値に必ずばらつきは生じます。

このばらつきを、我々は確率分布として表現します。確率分布とは、母集団(我々が知りたいと思う集団全体)の要素のばらつきの様子を規定したものと考えてください。

確率分布には色々な種類の分布がありますが、今回述べる正規分布はその確率分布の一つです。測定して得られるいわゆる計量値は、通常は正規分布に従うので、棒の長さも正規分布に従うと考えて問題ないことが多いです。もし、厳密な確認が必要であれば、ヒストグラムを作ったり、正規性の検定を行ったりします。

そして、正規分布に従うことを仮定できれば、母集団の姿を推定したり、確率を計算したりできるようになります。

例えば、金属棒の長さの平均値が100mm、標準偏差が2mmとしましょう。サンプルサイズを10本、100本、1000本、10000本とサンプリングして、得られた長さの測定値をそれぞれヒストグラムにしたものを、図1に示します。なお、ヒストグラムの柱の本数はn(n：サンプルサイズ)で決めています。

fig = plt.figure(figsize=(20, 5))

ax1 = fig.add_subplot(1, 4, 1)
ax2 = fig.add_subplot(1, 4, 2)
ax3 = fig.add_subplot(1, 4, 3)
ax4 = fig.add_subplot(1, 4, 4)

ax1.hist(data1, bins=int(10**0.5))
ax1.set_title("n=10")

ax2.hist(data2, bins=int(100**0.5))
ax2.set_title("n=100")

ax3.hist(data3, bins=int(1000**0.5))
ax3.set_title("n=1000")

ax4.hist(data4, bins=int(10000**0.5))
ax4.set_title("n=10000")

plt.show()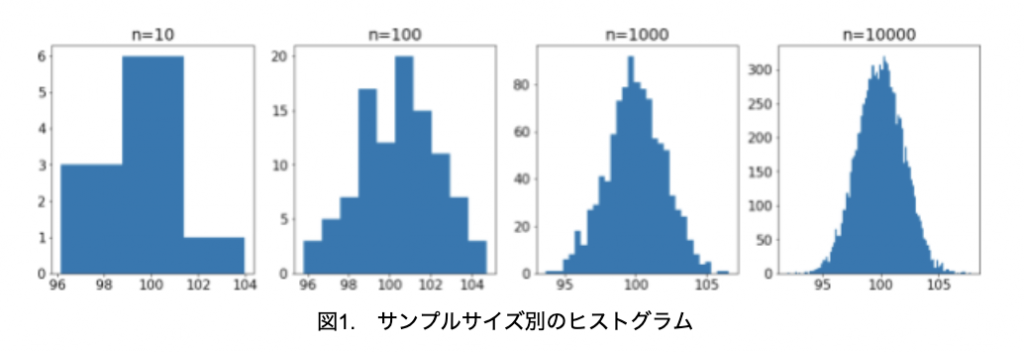

サンプルサイズが小さいとヒストグラムの形状は凸凹していますが、サンプルサイズを大きくして区間を狭くすると、左右対称の釣鐘状に近づくことがわかります。そして、サンプルサイズを無限大にすると、連続した曲線になります。これが正規曲線と呼ばれるもので、正規曲線に従う確率分布を正規分布と呼びます(図2)。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

X = np.arange(90,110,0.1)
Y = norm.pdf(x=X, loc=100, scale=2)

plt.plot(X,Y)
plt.ylim(0, 0.25)

plt.grid()
plt.show()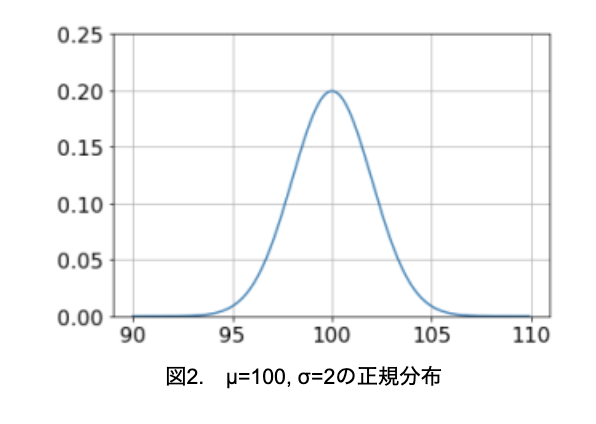

正規分布は以下の関数で表すことができます。

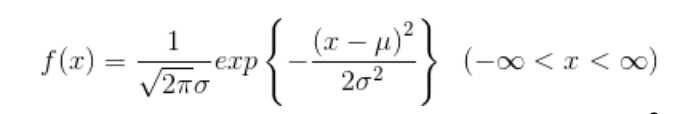
μは母集団の平均(母平均)、σは母集団の標準偏差(母標準偏差)で、μとσ(または、σ²：分散)が定まれば正規分布は一つに定まることが分かります。

2)　正規分布の性質

正規分布は母平均を中心に、左右対称の釣鐘上の形状をしています。つまり、平均値周辺の値の出る確率が高く、平均値から遠くなるほど、その値の出現確率は低くなっており、平均値、中央値(メジアン)、最頻値(モード)は一致するという特徴があります。

両端で0になっているように見えますが、数学上は0にはなっていません。そして、正規分布の内側の面積は1となります。

従って、ある値以上あるいは以下となる確率を求めたい場合は、面積を求めればその値がそのまま確率になることを意味します。

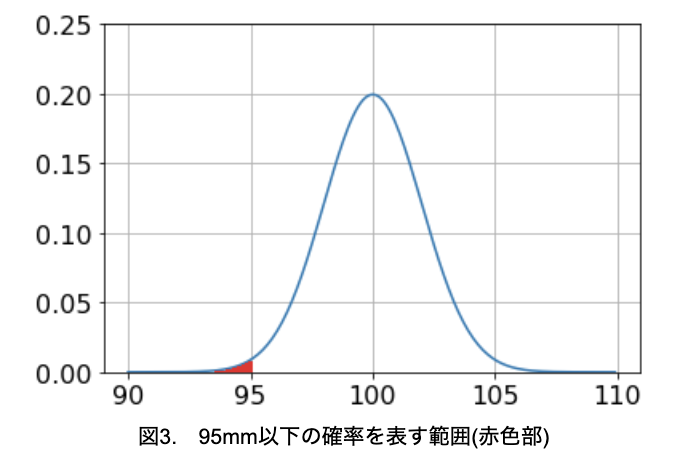
例えば、図2で95mm以下となる確率を求めたい場合、95と正規曲線で囲まれる部分の面積を計算すればよいのです(図3)。この場合、約0.6%という結果が得られます。

from scipy.stats import norm
 
prob = norm.cdf(x=95, loc=100, scale=2) 
print(prob)

0.006209665325776132

また、正規分布の性質の一つである中心極限定理も見ておきましょう。

中心極限定理とは、「x₁, x₂, …, x_nが独立に母平均μ、母分散σ²の同じ確率分布(正規分布でなくてもよい)に従う時、抽出するサンプルサイズnが大きいなら、標本平均x(サンプルの平均)の分布は平均μ、分散σ²/n(標準偏差σ/n)の正規分布に近似的に従う」というものです。

正規分布に従う母集団から抽出したサンプルの平均値が、正規分布に従うことは予想できますが、一様分布や指数分布など、正規分布に従わない母集団でも、サンプルの平均値が正規分布に従うと言うのは、意外に感じるかもしれません。

そこで、一様分布に従う母集団からサンプルを抜き取り、その平均値がどのような分布に従うか見てみましょう。

母集団として、50～100の範囲で一様分布に従う10000個のデータを仮定します(図4)。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(seed=1)
data = np.random.rand(10000) * 50 + 50 # 50〜100の乱数を1000個生成
data1 = np.round(data, decimals=1)

plt.hist(data)
plt.title("Uniform distribution(50 to 100)")
plt.show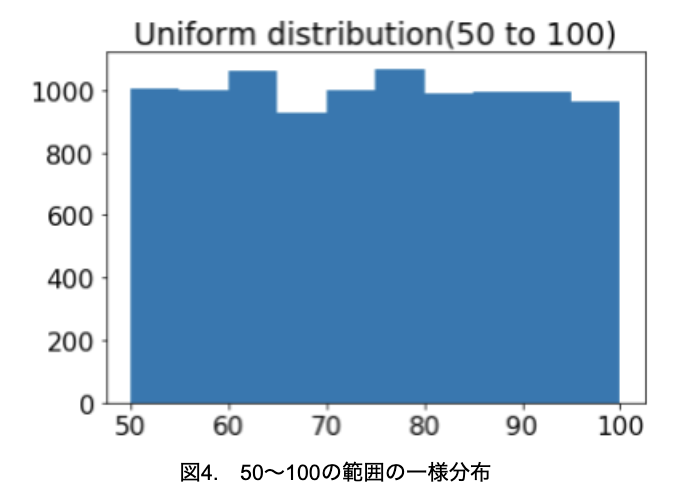

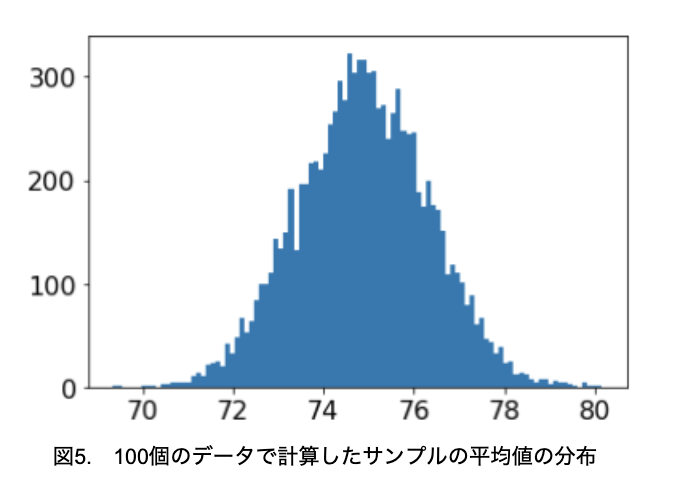
図4の分布に従う母集団から、100個抜き取って平均値を計算することを10000回繰り返し、得られた10000個のデータのヒストグラムを作成してみましょう(図5)。

np.random.seed(seed=1)

xbar=[]

for i in range(10000):
    x = np.random.choice(data1, size=100, replace=False)
    xbar.append(np.round(x.mean(), decimals=2))

plt.hist(xbar, bins=int(10000**0.5))
plt.show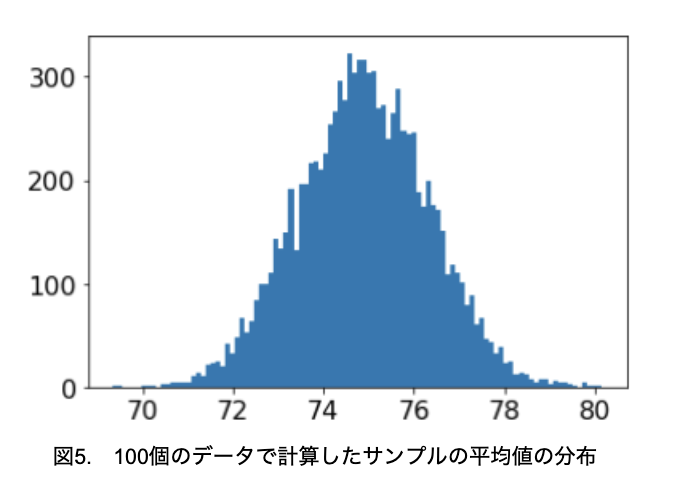

元の分布は一様分布ですが、サンプル100個の平均値の分布は正規分布に近いことが確認できました。

では、母集団(図4)と標本平均(図5)の平均値と標準偏差を計算しておきましょう。

print("母集団の平均値： {:.2f}".format(np.mean(data1)))
print("母集団の標準偏差： {:.3f}".format(np.std(data1)))

print("標本平均の平均値： {:.2f}".format(np.mean(xbar)))
print("標本平均の標準偏差： {:.3f}".format(np.std(xbar)))

母集団の平均値： 74.90
母集団の標準偏差： 14.385
標本平均の平均値： 74.88
標本平均の標準偏差： 1.442

母集団と標本平均は、まずまず一致していることが分かります。また、標本平均の標準偏差は、母平均の標準偏差の1/100=1/10となっていることが分かり、中心極限定理が成り立っていることが確認できました。

3)　データサイエンスにおける正規分布の重要性

これまで、正規分布について詳しく見てきましたが、正規分布はデータサイエンスとどう関係があるのでしょうか？実は、多くの統計的手法は正規分布を仮定しています。例えば、線形回帰分析であれば、予測値と実測値の差(残差)が正規分布に従うことを前提としています。従って、正規分布を前提とした手法は、正規分布以外の分布には使うことができません。

そのため、まず分布の形がどうなっているかを見ることは非常に重要で、正規分布を前提としたモデルを作るのであれば、データが正規分布に従うことを事前に確認しておく必要があるのです。